Primzahlen: Erklärung, Beispiele und Berechnung

Primzahlen werden hier behandelt. Dies sehen wir uns an:

• Erklärungen, was eine Primzahl ist und wie man eine Primzahl berechnet.
• Viele Beispiele zu Primzahlen.
• Aufgaben / Übungen zu diesem Thema.
• Ein Video zu Primzahlen.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Wir sehen uns gleich die Primzahlen an. Dabei werfen wir auch einen Blick darauf, wie man selbst prüft, ob eine Zahl eine Primzahl ist oder nicht. Um dies zu machen braucht man die Teilbarkeitsregeln. Mit diesen findet man heraus, ob eine Zahl durch eine andere Zahl oder Rest teilbar ist. Wer davon noch keine Ahnung hat, bitter kurz nachlesen.

Erklärung Primzahlen

Starten wir mit einer Erklärung zu Primzahlen. Zunächst sollte jeder verstehen, was das überhaupt ist. Eine Definition für eine Primzahl:

Die ersten Primzahlen lauten 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53.

Warum sind 0 und 1 keine Primzahlen?

Starten wir mit der Frage, warum 0 keine Primzahl ist? Dies ist relativ einfach, denn eine Zahl muss durch sich selbst teilbar sein. Dies ist bei der Null nicht der Fall, da man durch Null nicht teilen darf. Die Berechnung der Aufgabe 0 : 0 ist nicht erlaubt.

Und warum ist die 1 keine Primzahl? Nun, es gab Zeiten in der Mathematik, da hatte man die 1 als Primzahl angesehen. Denn die 1 lässt sich durch 1 und durch sich selbst ohne Rest teilen. Diese Kriterien sind somit erfüllt. Dennoch hat man sich im Laufe des letzten Jahrhunderts per Definition dazu entschieden die 1 nicht mehr als Primzahl anzusehen. Grund dafür war zum Beispiel, dass die 1 nur einen Teiler hat während die anderen Primzahlen zwei Teiler haben. Außerdem, wäre die Primfaktorzerlegung mit einer 1 dabei nicht eindeutig (Kurzinfo dazu weiter unten).

Wie prüft man, ob eine Zahl eine Primzahl ist?

Wie kann man herausfinden, ob eine Zahl eine Primzahl ist oder nicht? Dazu gibt es verschiedene Möglichkeiten einen Primzahltest durchzuführen. Ein einfaches Verfahren möchten wir hier kurz vorstellen. Die Vorgehensweise:

1. Man nimmt die zu untersuchende Zahl und zieht aus dieser die Wurzel.
2. Man schreibt sich auf, welche Primzahlen es bis zu dieser Zahl gibt
3. Diese Primzahlen auf die ursprüngliche Zahl anwenden und schauen, ob diese ohne Rest teilen.
4. Findet sich bis dahin keine Zahl findet, handelt es sich um eine Primzahl.

Beispiel 1:

Ist die Zahl 163 eine Primzahl?

Lösung:

Wir ziehen zunächst aus der Zahl 163 die Wurzel. Diese ist ungefähr 12,767.

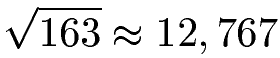
Bis zu dieser Zahl suchen wir alle Primzahlen raus (Blick an den Anfang des Artikels). Dies sind 2, 3, 5, 7 und 11. Wir nehmen nun die 163 und teilen durch all diese Primzahlen. Entsteht kein Rest (ist identisch mit Null hinter dem Komma) haben wir einen Teiler. Entsteht ein Rest (wir haben etwas hinter dem Komma ungleich Null stehen) ist die Primzahl kein Teiler. Rechnen wir dies einmal durch:

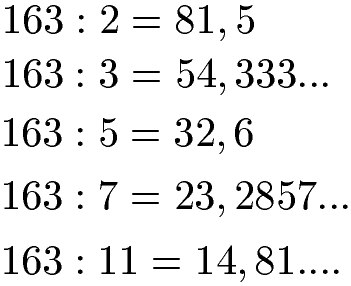
Wie man klar sehen kann: Nach dem Komma haben wir immer Zahlen stehen. Es gibt keine Division bei der nur Nullen hinter dem Komma stehen. Da dies bei allen Berechnungen der Fall war ist 163 eine Primzahl.

Beispiel 2:

Ist die Zahl 228 eine Primzahl?

Lösung:

Wir ziehen aus der Zahl 228 die Wurzel und erhalten in etwa 15,1.

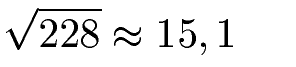
Bis zu dieser Zahl gibt es die Primzahlen 2, 3, 5, 7, 11 und 13. Daher nehmen wir die 228 und teilen sie durch diese Primzahlen. Entsteht irgendwo kein Rest haben wir keine Primzahl.

Wir man sehen kann, haben wir zwei Divisionen ohne Rest (grün eingerahmt). Aus diesem Grund ist 228 keine Primzahl.

Anzeige:

Primzahlen Beispiele / Listen

In diesem Abschnitt gibt es zahlreiche Beispiele zu Listen / Tabellen von Primzahlen. Diese Listen sind daher interessant, da manche Menschen direkt nach Listen von Primzahlen bis 50, 100 oder gar 1000 suchen.

Primzahlen bis 50:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47

Primzahlen bis 100:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Primzahlen bis 1000:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997

Anwendung von Primzahlen:

Wo werden denn Primzahlen überhaupt eingesetzt? Dazu einige Beispiele:

• Primfaktorzerlegung: Bei den Primfaktoren bzw. der Primfaktorzerlegung geht es darum eine Zahl in möglichst kleine Multiplikationen von Primzahlen zu zerlegen. So kann man die Zahl 90 zerlegen in 90 = 2 · 5 · 3 · 3. Dabei sind 2, 5 und 3 jeweils Primzahlen.
• ggT: Das ggT steht für größer gemeinsamer Teiler. Dabei werden zwei Zahlen zerlegt und dann die größtmögliche gemeinsame Zahl gesucht. Als Beispiel könnte man die Zahlen 36 und 48 nehmen. Die Teiler von 36 sind 1, 2, 3, 4, 6, 9, 12, 18, 36 und die Teiler von 48 sind 1, 2, 3, 4, 6, 8, 12, 16, 24, 48. Die Zahl 12 ist die größte Zahl, die bei beiden Teilern vorkommt.
• kgV: Das kgV steht für kleinstes gemeinsames Vielfaches. Auch hier werden zwei Zahlen untersucht. Dabei wird jede Zahl mit 2, 3, 4 etc. multipliziert und aufgeschrieben. Im Anschluss wird nachgesehen, wo die kleinste gemeinsame Zahl zu finden ist. Als Beispiel soll das kgV von 12 und 18 ermittelt werden. Die Vielfachen von 12 sind 12, 24, 36, 48, 60 .... Die Vielfachen von 18 sind 18, 36, 54, 72, 90. Das kleinste gemeinsame Zahl ist somit die 36.

Aufgaben / Übungen Primzahlen

Aufgabe 1: Welche Aussage zur Zahl 0 stimmt?

• Ist eine Primzahl, da eine natürliche Zahl
• Keine Primzahl, da man nicht durch Null teilen darf
• Keine Primzahl, da man nicht durch 1 teilen kann
• Ist eine Primzahl, da durch Null teilbar

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Primzahlen

Fragen und Antworten Primzahl