Rechenvorteile nutzen / Vorteilhaftes Rechnen

Wie man Rechenvorteile nutzt wird in diesem Artikel behandelt. Dies sehen wir uns an:

• Eine Erklärung, worum es beim vorteilhaften Rechnen geht.
• Viele Beispiele um Rechenvorteile zu nutzen.
• Aufgaben / Übungen damit ihr dieses Thema selbst üben könnt.
• Einige Videos zum Rechnen mit Zahlen.
• Ein Frage- und Antwortbereich rund um dieses Thema.

Um überhaupt Rechenvorteile nutzen zu können, solltet ihr bereits einfache Additionen und Subtraktionen (also plus und minus), Multiplikationen (mal nehmen) und Divisionen (teilen) können. Wer hier noch Probleme hat, bitte erst einmal diese Themen lesen und die Aufgaben dazu behandeln.

Erklärung Rechenvorteile

Die Idee bei Rechenvorteilen ist eigentlich ganz einfach:

1. Kleine Aufgabe, große Aufgabe

Manchmal hat man Probleme eine Aufgabe mit größeren Zahlen zu rechnen. Eine Möglichkeit ist es dann die Aufgabe zu vereinfachen und erst einmal die vereinfachte Aufgabe zu lösen. Für 84 + 2 soll dies einmal bei einer Addition gezeigt werden:

• Große Aufgabe: 84 + 2 = 86
• Kleine Aufgabe: 4 + 2 = 6

Hier lässt man erst einmal die Zehnerstelle weg. Wir machen aus 84 + 2 erst einmal 4 + 2. Dies ergibt 6. Danach fügen wir noch die 8 von der 84 hinzu. Damit können wir die große Aufgabe 84 + 2 = 86 lösen.

Die Idee mit der kleinen Aufgabe kann man auch bei der Subtraktion einsetzen. Auch hier nehmen wir für die kleine Aufgabe die Zehnerstelle erst einmal raus, rechnen also nur mit der Einerstelle. Sehen wir uns dies für 18 - 4 an:

• Große Aufgabe: 18 - 4 = 14
• Kleine Aufgabe: 8 - 4 = 4

2. Aufgabe verändern

Eine weitere Möglichkeit Rechenvorteile zu nutzen besteht darin eine Aufgabe zu verändern, damit man mit den Zahlen einfacher rechnen kann. Machen wir dies einmal mit 56 + 38.

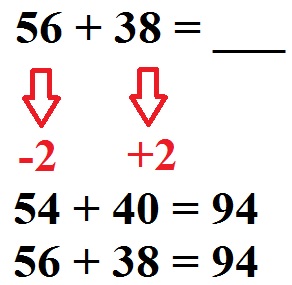
Mit 56 + 38 haben einige vielleicht Probleme. Aber was ändert sich am Ergebnis, wenn ich daraus 54 + 40 machen? Nichts. Daher machen wir dies, in dem wir einmal 2 Subtrahieren und einmal 2 Addieren. Die Berechnung 54 + 40 = 94 dürfte vielen Menschen einfacher fallen.

Dies funktioniert natürlich auch bei der Subtraktion. Zu sehen an 62 - 48:

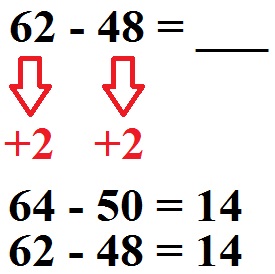
Hier addieren wir jeweils 2 drauf um 64 - 50 zu erhalten. Das Ergebnis 14 gilt dann für die vereinfachte Aufgabe wie auch für die ursprüngliche Aufgabe.

3. Kommutativgesetz, Assoziativgesetz

Sehen wir uns als nächstes ein Rechengesetz an. Das Kommutativgesetz kann man bei Additionen und auch bei Multiplikationen einsetzen. Im Deutschen wird dieses oftmals als Vertauschungsgesetz bezeichnet. Dies macht auch Sinn, denn man kann die Zahlen bei der Addition und Multiplikation vertauschen ohne dabei am Ergebnis etwas zu ändern.Manchen fällt es nach dem Vertauschen einfacher eine Aufgabe zu lösen. Beim Assoziativgesetz darf man die Summmanden beliebig zusammenfassen.

Für die Addition:

• 3 + 4 = 7
• 4 + 3 = 7

• 8 + 9 = 17
• 9 + 8 = 17

Für die Multiplikation:

• 4 · 5 = 20
• 5 · 4 = 20

• 6 · 2 = 12
• 2 · 6 = 12

Dadurch ergeben sich manchmal Rechenvorteile:

• 12 + 18 + 8 + 2 = ____
• 12 + 8 + 18 + 2 = ____
• 20 + 20 = 40

In diesem Fall kann man die Zahlen so umordnen, dass jeweils 20-iger Päckchen entstehen und man damit einfacher auf die 40 als Summe kommt.

4. Distributivgesetz

Mit dem Distributivgesetz kann ein konstanter Faktor ausgeklammert werden.

• a · b + a · c = a · (b + c)

Bedeutet zum Beispiel:

• a = 3
• b = 8
• c = 5
• 3 · 8 + 3 · 5 = 39
• 3 · (8 + 5) = 39

Dies hilft vor allem bei längeren Aufgaben mit konstantem Faktor:

• 3 · 5 + 3 · 6 + 3 · 7 = ____
• 3 · (5 + 6 + 7) = ____
• 3 · 18 = 54

Beispiele Rechenvorteile

In diesem Abschnitt sollen noch einige Beispiele zum vorteilhaften Rechnen gezeigt werden.

Beispiel 1:

Nutze Rechenvorteile um die Aufgabe 88 + 112 zu berechnen.

Lösung:

• 88 + 112 = ____
• 90 + 110 = 200

Beispiel 2:

Löse 73 + 98 + 27 + 2 auf möglichst einfache Art und Weise.

• 73 + 98 + 27 + 2 = ____
• 73 + 27 + 98 + 2 = 200

Beispiel 3:

Nutze Rechenvorteile zum Lösen von 7 · 8 + 3 · 8 + 5 · 8.

Lösung:

• 7 · 8 + 3 · 8 + 5 · 8 = ____
• 8 · (7 + 3 + 5) = ____
• 8 · 15 = 120

Nun seid ihr dran. Macht unsere Aufgaben bzw. Übungen zu Rechenvorteilen (vorteilhaftes Rechnen) und versucht dabei selbst auf die richtigen Ergebnisse zu kommen.

Übungsaufgaben Rechenvorteile

Videos Rechenvorteile

Fragen mit Antworten Rechenvorteile