Rechendreieck: Erklärung und Beispiele

Das Rechendreieck wird in diesem Artikel behandelt. Dies sehen wir uns an:

• Eine Erklärung, was eine Rechendreieck ist und wie man es löst.
• Viele Beispiele zum Lösen eines Rechendreiecks.
• Aufgaben / Übungen damit ihr selbst das Rechendreieck üben könnt.
• Ein Video zum Thema Rechendreieck.
• Ein Frage- und Antwortbereich rund um dieses Thema.

Wir sehen uns hier gleich das Rechendreieck an. Viele Vorkenntnisse sind nicht nötig. Wem sie dennoch wichtig sind: Für Aufgaben mit kleineren Zahlen reicht es einfache Additionen und Subtraktionen durchzuführen. Bei größeren Zahlen helfen euch schriftliche Addition und schriftliche Subtraktion.

Erklärung Rechendreieck

Einfache Additionen und Subtraktionen sind auf Dauer einfach langweilig. Aus diesem Grund werden diese in der Grundschule - und manchmal auch danach - in Form von Rechendreiecken optisch etwas ansprechender gezeigt. Fangen wir ganz einfach an.

Rechendreiecke bis 20:

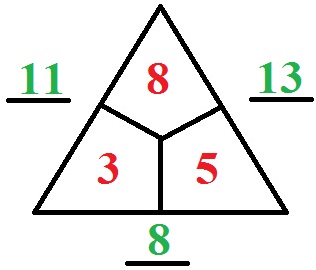
Ganz einfache Rechendreiecke werden oftmals schon in der 1. Klasse oder 2. Klasse der Grundschule behandelt. Der Aufbau ist ganz einfach: Wir haben innen drei Felder und außen drei Striche. Auf den Strichen außen stehen die Summen der Zahlen innen. Für das nächste Rechendreieck sieht dies so aus:

• 3 + 8 = 11
• 3 + 5 = 8
• 8 + 5 = 13

Rechendreiecke bis 100 und 1000:

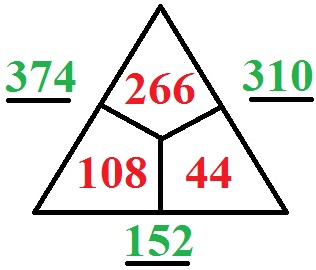
In der 2. Klasse, 3. Klasse und auch 4. Klasse der Grundschule werden Rechendreiecke im Zahlenraum bis 100 oder gar bis 1000 behandelt. Auch hier sehen wir uns noch ein Rechendreieck an, bevor wir an die Beispiele zum Rechnen kommen. Bis 1000 sieht dies so aus:

• 108 + 266 = 374
• 266 + 44 = 310
• 108 + 44 = 152

Im nächsten Abschnitt sehen wir uns Beispiele an, wie sie gerne Lehrer in der Schule stellen.

Anzeige:

Beispiele Rechendreieck

Sehen wir uns nun Aufgaben an, wie sie oft in der Schule gestellt werden.

Beispiel 1:

Fülle das nächste Rechendreieck aus:

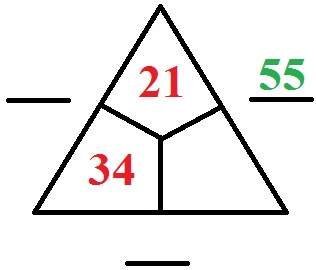
Lösung:

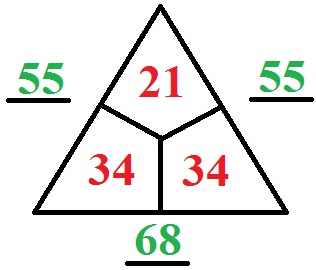
• Auf der linken Seite können wir die Zahl durch Addition finden. 21 + 34 = 55.
• Rechts unten finden wir die Zahl durch folgende Überlegung: 21 + ____ = 55. Wir kehren um und erhalten: 55 - 21 = 34.
• Fehlt noch der Strich unten: 34 + 34 = 68.

Beispiel 2 ohne innere Zahlen:

Jetzt machen wir noch etwas ganz spezielles. Die folgende Aufgabe wird normalerweise nicht in der Grundschule gestellt, denn hier ist der Umgang mit Gleichungen gefragt. Wer dennoch neugierig ist, liest dennoch weiter: Wir haben jetzt ein Rechendreieck ohne innere Zahlen. Drei Zahlen außen sind gegeben und drinnen fehlen eben die drei Zahlen. Für die drei fehlenden Zahlen innen habe ich einmal drei Variablen (a, b und c) als Platzhalter vorgesehen. Das Rechendreieck ohne innere Zahlen sieht dann so aus:

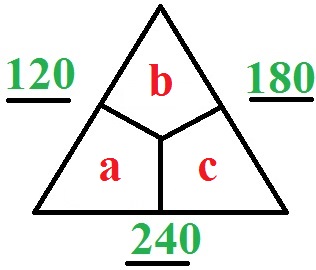
Lösung:

Wie löst man eine Aufgabe ohne innere Zahlen nun? Die erste Möglichkeit wäre einfach einmal irgendwelche Zahlen einzusetzen und zu schauen, ob es am Ende passt. Das ist allerdings keine sonderlich "mathematische" Lösung. Wir können jedoch Gleichungen aufstellen.

Wir wissen, dass wenn wir die Zahlen bei a und b addieren 120 rauskommen muss. Die Zahlen bei b und c zusammen müssen 180 ergeben und a und c zusammen müssen 240 ergeben. Die Gleichungen sehen also so aus:

• a + b = 120
• b + c = 180
• a + c = 240

Wir haben drei Gleichungen mit drei Unbekannten (a, b und c). So etwas kann man berechnen. Dazu müssen wir die Gleichungen umstellen. Zunächst die zweite Gleichung durch Subtraktion von c nach b umstellen:

• b + c = 180
• b = 180 - c

Und auch die dritte Gleichung stellen wir durch Subtraktion von c nach a um:

• a + c = 240
• a = 240 - c

Wir wissen, dass b = 180 - c ist und a = 240 - c. Dies setzen wir nun in die 1. Gleichung ein, vereinfachen und berechnen c.

• a + b = 120
• 240 - c + 180 - c = 120
• 420 - 2c = 120
• -2c = -300
• c = 150

Wir erhalten c = 150. Da b + c = 180 sein soll muss b = 30 sein. Und b + a = 120 bringt uns a = 90.

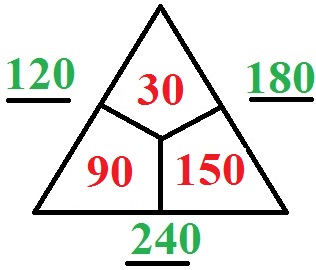
Übungsaufgaben Rechendreieck

Aufgabe 1: Bevor ihr selbst mit dem Rechnen anfangt eine ganz kurze Frage zum Rechendreieck. Was stehen außerdem des Rechendreiecks normalerweise für Zahlen?

• Das Produkt zweier Zahlen
• Der Quotient zweier Zahlen
• Die Summe zweier Zahlen
• Die Differenz zweier Zahlen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Rechendreieck

Fragen mit Antworten Rechendreieck