Ungleichnamige Brüche
Geschrieben von: Dennis RudolphDienstag, 20. April 2021 um 17:05 Uhr
Was ungleichnamige Brüche sind, wie man diese gleichnamig macht und wie man mit diesen rechnet lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, was ein ungleichnamiger Bruch ist.
- Viele Beispiele zum Rechnen mit ungleichnamigen Brüchen.
- Aufgaben / Übungen zur Bruchrechnung.
- Videos zur Addition und Subtraktion von Brüchen.
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Ein kleiner Tipp zum Start: Wenn ihr nicht wisst, was ein Bruch ist, werft bitte erst einmal einen Blick in den Hauptartikel Bruchrechnen. Ansonsten sehen wir uns nun ungleichnamige Brüche an.
Erklärung ungleichnamige Brüche
Noch einmal eine ganz kurze Erinnerung zum Aufbau von einem Bruch. Über dem Bruchstrich steht der Zähler und darunter der Nenner.
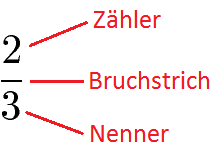
Kommen wir nun zum Unterschied zwischen gleichnamigen und ungleichnamigen Brüchen.
Haben Brüche den gleichen Nenner, dann bezeichnet man diese Brüche als gleichnamig. Sind die Nenner verschieden nennt man die Brüche ungleichnamig.
Zum besseren Verständnis ein paar Beispiele. Die nächsten Brüche sind gleichnamig:
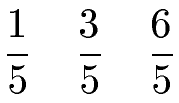
Im Vergleich dazu ein paar ungleichnamige Brüche. Man erkennt dies daran, dass alle Nenner verschieden sind.
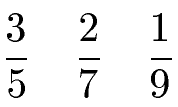
Das Problem bei ungleichnamigen Brüchen besteht darin, dass man mit diesen nicht so einfach Brüche addieren, Brüche subtrahieren oder Brüche vergleichen kann. Daher muss man ungleichnamige Brüche gleichnamig machen. Für die Multiplikation und Division von Brüchen spielt es keine Rolle, ob die Brüche gleichnamig oder ungleichnamig sind.
Anzeigen:
Beispiele ungleichnamige Brüche rechnen
Wie kann man ungleichnamige Brüche gleichnamig machen? Oder anders ausgedrückt: Wie kann man alle Brüche auf den gleichen Nenner bringen? Dazu sehen wir uns ein paar Beispiele zur Addition und Subtraktion von Brüchen und auch Vergleiche an.
Beispiel 1:
Zwei ungleichnamige Brüche sollen addiert werden. Wie können diese gleichnamig gemacht werden? Wie lautet das Ergebnis (Summe)?
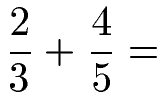
Lösung:
Wir haben hier ungleichnamige Brüche, sprich die Nenner sind verschieden. Wir müssen daraus gleichnamige Brüche machen. Wir erhalten mit 3 · 5 = 15 einen Hauptnenner.
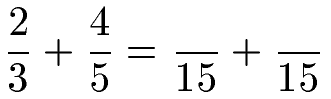
Fehlen uns noch die passenden Zähler. Beim ersten Nenner haben wir mit 5 im Nenner multipliziert, um auf 15 zu kommen. Dies machen wir nun auch im Zähler. Beim zweiten Bruch haben wir mit 3 im Nenner multipliziert, um auf 15 zu kommen. Daher machen wir dies nun auch im Zähler.
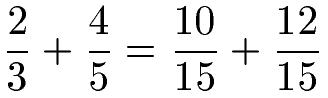
Wir addieren jetzt einfach die Zähler und behalten den Nenner bei:
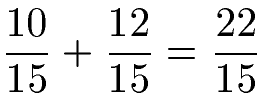
Beispiel 2:
Die Subtraktion von ungleichnamigen Brüchen steht in diesem Beispiel an. Auch hier soll für gleiche Nenner gesorgt werden, damit subtrahiert werden kann.
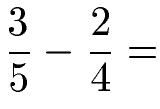
Lösung:
Den gemeinsamen Nenner erhalten wir, indem wir beide Ausgangsnenner miteinander multiplizieren: 5 · 4 = 20.
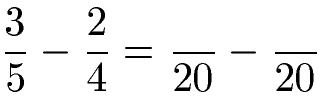
Jetzt passen wir die Zähler an. Beim ersten Bruch hatten wir den Nenner mit 4 multipliziert um auf die 20 zu kommen. Dies machen wir auch im Zähler: 3 · 4 = 12. Der zweite Nenner wurde mit 5 multipliziert um auf 20 zu kommen. Dies machen wir auch im Zähler: 2 · 5 = 10.
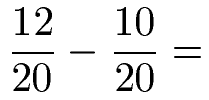
Für das Ergebnis subtrahieren wir die Zähler. Der gemeinsame Nenner wird in das Ergebnis übernommen.
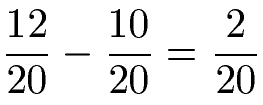
Wer mag kann diesen Bruch noch auf 1/10 kürzen.
Beispiel 3:
Um zwei Brüche miteinander zu vergleichen bringt man diese ebenfalls auf einen gemeinsamen Nenner. Welcher der beiden Brüche ist größer?
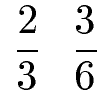
Lösung:
Wir müssen hier nicht die beiden Brüche miteinander multiplizieren für einen gemeinsamen Nenner. Hier reicht ein kritischer Blick auf beide Nenner, um zu sehen, dass die 6 ein Vielfaches der 3 ist. Daher können wir den ersten Bruch in Zähler und Nenner mit 2 multiplizieren.
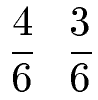
Um zu vergleichen müssen wir nur noch die Zähler betrachten. Die 4 ist größer als die 3. Daher ist der erste Bruch größer als der zweite Bruch.
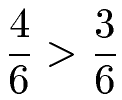
Bruchrechnung Übungsaufgaben
Anzeigen:Video ungleichnamiger Bruch
Beispiele und Erklärungen
Mit ungleichnamigen Brüchen befassen wir uns in diesem Artikel. Dies sind die Inhalte:
- Was ist ein gleichnamiger Bruch?
- Was ist ein ungleichnamiger Bruch?
- Beispiele.
- Erklärungen.
- Zähler und Nenner erkennen.
Nächstes Video »
Fragen mit Antworten zu ungleichnamigen Brüchen
In diesem Abschnitt geht es noch um typische Fragen mit Antworten zu ungleichnamigen Brüchen.
F: Können bei gleichnamigen und ungleichnamigen Brüchen auch Variablen vorkommen?
A: Natürlich können bei beiden Brucharten auch Variablen vorkommen. Die nächsten Brüche sind gleichnamig.
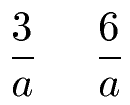
F: Muss man beim Multiplizieren und Dividieren ungleichnamige Brüche auf gleichnamig umwandeln?
A: Nein. Bei der Multiplikation oder Division von Brüchen spielt es keinerlei Rolle, ob die Brüche gleichnamig oder ungleichnamig sind.
F: Wann wir dieses Thema in der Schule behandelt?
A: Die Bruchrechnung wird meistens in der 5. Klasse oder 6. Klasse begonnen. Dabei geht es zunächst darum, was ein Bruch überhaupt ist. Die Grundrechenarten werden ebenfalls behandelt. Das Thema gleichnamige und ungleichnamige Brüche steht meistens in der 6. Klasse auf dem Plan.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
