Winkelarten, Winkelnamen, Größen und Typen

Mit Winkelarten bzw. Winkeltypen für verschiedene Größen und Typen von Winkeln, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wie man verschieden große Winkel benennt.
• Beispiele zu unterschiedlichen Winkeltypen und Winkelnamen.
• Aufgaben / Übungen damit ihr dies alles selbst üben könnt.
• Ein Video zu Winkelarten und Winkeltypen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier vieles zu Winkeln an. Jetzt hilft es, wenn ihr schon wisst, was ein Winkel überhaupt ist. Wer noch nicht weiß was ein Winkel ist sieht bitte in unseren Startartikel Was ist ein Winkel?

Erklärung Winkelarten und Winkeltypen

Winkel werden meistens in Grad - auch Altgrad genannt - angegeben. Diese gehen von 0° bis 360° wobei 360° ein kompletter Kreis ist. Werfen wir einen Blick auf die Winkelarten bzw. Winkeltypen. Mit diesem Wissen kann man Winkelarten bestimmen. Sehen wir uns also alle sieben Winkelnamen an.

Nullwinkel:

Liegen zwei Geraden, Halbgeraden, Strecken oder Schenkel direkt aufeinander, so sieht man als Betrachter gar keinen Winkel. Der Winkel ist somit 0°. Man bezeichnet dies auch als Nullwinkel. Die nächste Grafik zeigt einen Nullwinkel mit α = 0.

Spitzer Winkel:

Ist ein Winkel größer als 0 Grad aber kleiner als 90 Grad bezeichnet man diesen als spitzen Winkel. Man schreibt dies meistens in dieser Form auf: 0 < α < 90°. Das nächste Bild zeigt die Winkelart spitzer Winkel.

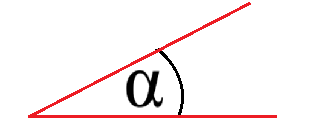
Rechter Winkel:

Ist ein Winkel exakt 90° groß, bezeichnet man diesen als rechten Winkel. Der rechte Winkel ist eine wichtige Winkelart in späteren Klassenstufen (bei Themen wie der analytischen Geometrie). Ein rechter Winkel entspricht 1/4 von einem Kreis. Das nächste Bild zeigt α = 90°.

Stumpfer Winkel:

Überschreitet die Winkelgröße 90 Grad - bleibt aber unter 180 Grad - dann liegt ein stumpfer Winkel vor. Der stumpfe Winkel ist damit größer als der rechte Winkel, aber kleiner als ein Halbkreis. Für den stumpfen Winkel gilt 90° < α < 180°. Dieser sieht so aus:

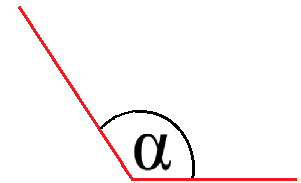
Gestreckter Winkel:

Ein Winkel der genau 180 Grad groß ist nennt man gestreckter Winkel. Dies entspricht einem halben Kreis. Die Winkelgröße lautet damit α = 180°. Um dies optisch besser darzustellen, setzt die nächste Grafik auf zwei verschiedene Farben.

Überstumpfer Winkel:

Wird die Winkelgröße von 180 Grad überschritten - bleibt aber unter 360 Grad - spricht man von einem überstumpfen Winkel. Man drückt dies mit 180° < α < 360° aus. Die nächste Grafik zeigt einen überstumpfen Winkel.

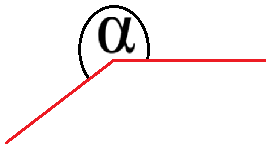
Vollwinkel:

Bleibt noch der Vollwinkel mit 360 Grad. Das entspricht einem kompletten Kreis. Diese Winkelart wird mit α = 360° beschrieben. Die nächste Grafik zeigt dies:

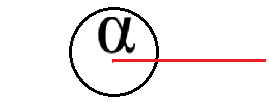
Anzeige:

Beispiele Winkelnamen und Winkeltypen

In den nächsten Abschnitten kommen mehr als ein Winkel pro Zeichnung vor. Daher brauchen wir auch mehr als einen Namen für die Winkel. Aus diesem Grund sehen wir uns erst einmal eine kleine Übersicht zu verschiedenen Winkelnamen in der Mathematik an.

Typische Winkelnamen:

Winkel an schneidenden Geraden:

Schneiden sich zwei Geraden (in rot eingezeichnet) entstehen dabei vier Winkel:

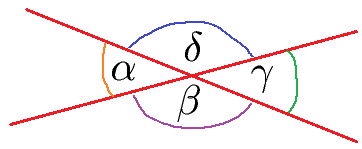
Man kann dabei Scheitelwinkel und Nebenwinkel finden.

Scheitelwinkel:

• Die gegenüberliegenden Winkel sind Scheitelwinkel.
  • Alpha (α) und Gamma (γ) sind Scheitelwinkel.
  • Beta (β)und Delta (δ)sind Scheitelwinkel.
• Scheitelwinkel sind gleich groß.

Nebenwinkel:

• Zwei Winkel die nebeneinander liegen sind Nebenwinkel.
  • Alpha (α) und Beta (β) sind Nebenwinkel.
  • Beta (β) und Gamma (γ) sind Nebenwinkel.
  • Gamma (γ) und Delta (δ) sind Nebenwinkel.
  • Delta (δ) und Alpha (α) sind Nebenwinkel.
• Die Summe zweier Nebenwinkel ergeben 180° (halber Kreis).

Winkel an geschnittenen Parallelen:

Werden zwei parallele Geraden geschnitten, entstehen ebenfalls mehrere Winkel. Man unterschiedet dabei Stufenwinkel und Wechselwinkel.

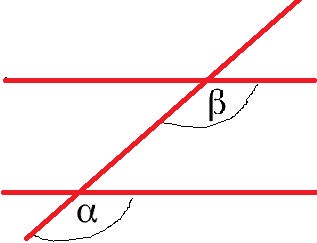
Stufenwinkel:

In der nächsten Grafik sind Alpha (α) und Beta (β) Stufenwinkel. Die Stufenwinkel sind gleich groß.

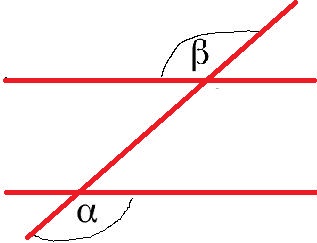
Wechselwinkel:

In der nächsten Grafik ist mit Alpha (α) und Beta (β) Wechselwinkel.

Aufgaben / Übungen zu Winkelarten

Aufgabe 1: Wie viel Grad hat ein rechter Winkel?

• 180 Grad
• 90 Grad
• 45 Grad
• 360 Grad

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 12 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Winkelarten

Fragen mit Antworten zu Winkeltypen