Brüche erweitern: Zahlen und Variablen

Das Erweitern von Brüchen lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wie man Brüche mit Zahlen und auch Variablen erweitern kann.
• Viele Beispiele zum Erweitern von Brüchen.
• Aufgaben / Übungen damit ihr selbst üben könnt.
• Ein Video zu diesem Thema.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Ein kleiner Tipp zu Beginn: Wenn ihr nicht wisst, was ein Bruch ist, werft bitte erst einmal einen Blick in den Hauptartikel Bruchrechnen.

Erklärung Brüche erweitern

Sehen wir uns kurz an, wie man einen Bruch rechnerisch erweitert und warum man einen Bruch überhaupt erweitert.

Aber was bedeutet dies? Nehmen wir eine Pizza und teilen diese in 2 gleich große Stücke. Die eine Hälfte ist in der nächsten Grafik in grün markiert und die andere Hälfte ist rot.

Natürlich könnte man aus der Pizza noch mehr Stücke machen. Nehmen wir jetzt an wir schneiden die Pizza in 8 gleich große Stücke. Auch hier ist es möglich 4 Stücke in grün darzustellen und 4 Stücke in rot. Dennoch ist die Hälfte der Pizza nun rot und die andere Hälfte grün.

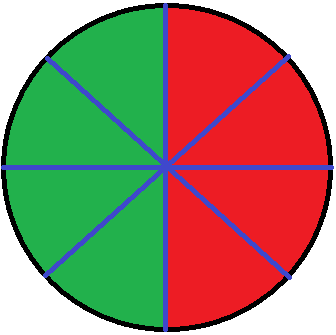
Aus 1 von 2 gleich großen Stücken haben wir 4 von 8 gleich große Stücke gemacht. Exakt dies passiert beim Erweitern von einem Bruch.

Wie berechnet man dies? Sehen wir uns dazu kurz ein paar Regeln / Hinweise zum Erweitern von Brüchen an.

Anzeige:

Beispiele Brüche erweitern

Machen wir zum Start ein einfaches Beispiel zur Brucherweiterung.

Beispiel 1:

Der folgende Bruch soll mit 2 erweitert werden. Wie lautet die Lösung?

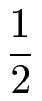
Lösung:

Einen Bruch mit 2 erweitern bedeutet, den Zähler und den Nenner jeweils mit 2 zu multiplizieren. Aus 1 : 2 wird dadurch 2 : 4.

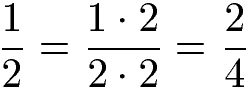
Beispiel 2:

Ein Bruch kann auch mit einer negativen Zahl erweitert werden. Das nächste Beispiel soll mit (-3) erweitert werden.

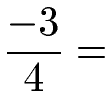
Lösung:

Wir multiplizieren den Zähler und den Nenner mit (-3). Man sollte dabei beachten, dass wenn man zwei negative Zahlen miteinander multipliziert, dass man dann im Ergebnis eine positive Zahl erhält. Ist einer der beiden Faktoren negativ ist auch das Ergebnis negativ.

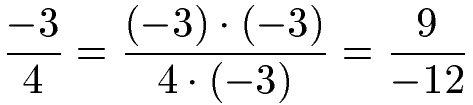
Beispiel 3:

Im dritten Beispiel soll mit Variablen erweitert werden. Um dies gleich ein bisschen komplizierter zu machen, soll der Bruch nicht einfach mit x oder y erweitert werden, sondern es soll hier gleich mit (x + y) erweitert werden. Der Bruch soll erst erweitert und dann ausmultipliziert werden.

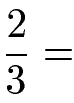
Lösung:

Wir multiplizieren Zähler und Nenner jeweils mit (x + y). Im Anschluss multiplizieren wir aus. Dazu multiplizieren wir alles in der Klammer mit der 2 oder 3 davor.

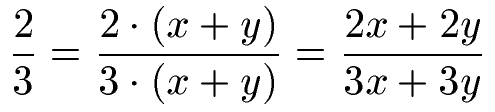
Beispiel 4:

Wo kann man die Erweiterung von Brüchen einsetzen? Antwort: Zum Beispiel bei der Addition von zwei Brüchen mit unterschiedlichem Nenner. Im nächsten Beispiel sollen zwei Brüche addiert werden. Wie lautet die Lösung?

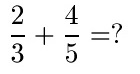
Lösung:

Die Nenner der beiden Brüche sind verschieden. Um einen gemeinsamen Hauptnenner für die beiden Brüche zu finden multiplizieren wir die beiden Nenner miteinander. Wer erhalten damit 3 · 5 = 15.

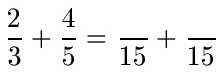
Die zugehörigen Zähler müssen noch berechnet werden. Beim ersten Nenner haben wir mal 5 im Nenner gerechnet, um auf 15 zu kommen. Im Zähler müssen wir dies auch tun. Beim zweiten Nenner haben wir mit 3 im Nenner multipliziert. Dies machen wir nun auch im Zähler.

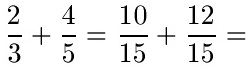
Jetzt einfach die beiden neuen Zähler addieren. Der Nenner bleibt:

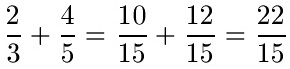
Übungsaufgaben Brüche erweitern

Aufgabe 1: Erweitere den nächsten Bruch mit 2. Wie lautet die Lösung?

• 3 : 4
• 1 : 2
• 2 : 4
• 4 : 2

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Brüche erweitern

Fragen mit Antworten Brüche erweitern