Bruch kürzen: Erklärung und Beispiele

Das Kürzen von Brüchen lernst du hier. Dies sehen wir uns an:

• Eine Erklärung, was man unter dem Kürzen von Brüchen versteht.
• Viele Beispiele zum Kürzen von Brüchen.
• Aufgaben / Übungen damit du selbst üben kannst.
• Ein Video zu diesem Thema.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Solltest du noch nicht wissen was ein Bruch ist, empfehle ich dir erst einmal einen Blick auf das Thema Bruchrechnen zu werfen. Ansonsten ran an das Kürzen von Brüchen.

Erklärung Brüche kürzen

Brüche zu kürzen bedeutet Brüche zu vereinfachen. Ein Bruch wird gekürzt, indem der Zähler und der Nenner des Bruchs durch die gleiche Zahl geteilt wird. Am Wert des Bruchs ändert sich dabei nichts.

Das Kürzen von Brüchen kannst du dir sehr einfach mit einer Pizza vorstellen. Diese zerschneiden wir in 8 Stücke, die alle gleich groß sind. Jetzt essen wir 4 der 8 Stücke auf. Der Bruch sieht damit so aus:

Dies könnte man auch so darstellen, dass wir 4 der 8 Stücke in grün darstellen und die restlichen 4 Stücke in rot.

4 von 8 Stücken wurden gegessen. Die halbe Pizza. Genau dies lässt sich jedoch auch darstellen durch 1 von 2 Stücken. Auch in diesem Fall wurde die halbe Pizza gegessen.

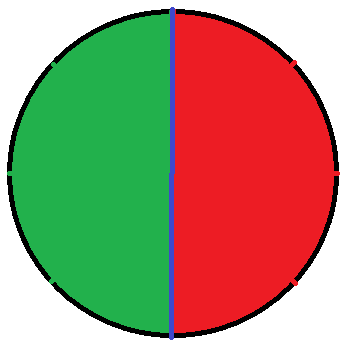
Der Bruch wurde von 4 von 8 auf 1 von 2 gekürzt. In der Bruchschreibweise wird dies wie folgt geschrieben.

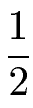
Durch das Kürzen eines Bruches ändert sich dessen Wert nicht. Es ist eine halbe Pizza, egal ob mit 4 von 8 oder 1 von 2 Stücken.

Anzeige:

Brüche kürzen mit Teilbarkeitsregeln

Ein Bruch wird gekürzt, indem man Zähler und Nenner durch die gleiche Zahl teilt. Zum Beispiel könnte man Zähler und Nenner durch 2, 3, 4 etc. teilen. Ob eine Zahl durch eine andere Zahl ohne Rest geteilt werden kann, erfährst du durch die Teilbarkeitsregeln. Diese besagen:

• Teilbarkeitsregel 2: Eine Zahl ist durch 2 teilbar wenn diese auf 0, 2, 4, 6 oder 8 endet.
• Teilbarkeitsregel 3: Eine Zahl ist durch 3 teilbar, wenn ihre Quersumme durch 3 teilbar ist.
• Teilbarkeitsregel 4: Eine Zahl ist durch 4 teilbar, wenn die letzten beiden Stellen der Zahl durch 4 teilbar sind.
• Teilbarkeitsregel 5: Eine Zahl ist durch 5 teilbar, wenn die letzte Stelle eine 0 oder 5 ist.
• Teilbarkeitsregel 6: Eine Zahl ist durch 6 teilbar wenn diese durch 2 und durch 3 teilbar ist. Wende dazu die Teilbarkeitsregeln für 2 und 3 an.
• Teilbarkeitsregel 8: Eine Zahl ist durch 8 teilbar, wenn die letzten drei Stellen durch 8 teilbar sind.
• Teilbarkeitsregel 9: Eine Zahl ist durch 9 teilbar, wenn die Quersumme durch 9 teilbar ist.
• Teilbarkeitsregel 10: Eine Zahl ist durch 10 teilbar, wenn die Einerstelle eine 0 ist.

Weitere Teilbarkeitsregeln und Beispiele findest du unter Teilbarkeitsregeln. Mit diesen Regeln zur Teilbarkeit lassen sich Brüche kürzen. Wir untersuchen Zähler und Nenner nach gemeinsamen Teilern und kürzen mit diesen. Dazu einige Beispiele.

Beispiel 1: Kürzen mit 2

Bei den nächsten Brüchen wurde mit 2 gekürzt. Anders ausgedrückt: Zähler und Nenner wurden jeweils durch 2 geteilt.

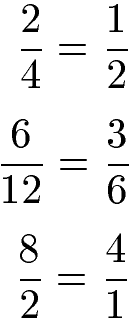
Beispiel 2: Kürzen mit 3

Es folgen noch drei Beispiele bei denen mit 3 gekürzt wurde. Zähler und Nenner wurden jeweils durch 3 geteilt.

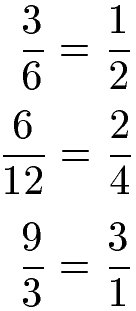
Brüche kürzen: Zahlen und Variablen

Brüche mit großen Zahlen oder Variablen zu kürzen erfordert meistens mehrere Rechenschritte. Ziel ist es, einen Bruch vollständig zu kürzen. Vollständig kürzen bedeutet, dass es keine natürliche Zahl mehr gibt, durch die Zähler und Nenner noch geteilt werden können. Ein vollständig gekürzter Bruch befindet sich in der Grunddarstellung. Hier lernst du nun mit Beispielen wie dies funktioniert.

Beispiel 3: Großen Bruch vollständig kürzen

Der nächste Bruch soll vollständig gekürzt und damit in Grunddarstellung gebracht werden.

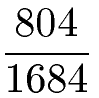
Lösung: Im Zähler und im Nenner haben wir jeweils gerade Zahlen, daher können wir beide durch 2 ohne Rest teilen. Auch bei 402 : 842 kannst du dies wiederholen und erneut durch 2 teilen. Bei 201 : 421 sind wir mit dem Kürzen vollständig.

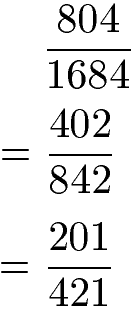
Beispiel 4: Bruch mit Variablen

Ist eine Zahl noch nicht bekannt, wird an deren Stelle ein Platzhalter gesetzt. In der Mathematik ist diese eine Variable (= Buchstabe). Auch hier kann in einigen Fällen gekürzt werden. Ein einfaches Beispiel soll hier gezeigt werden. Dabei findet sich ein x in Zähler und Nenner (jeweils mit nur Multiplikationen) und daher darf gekürzt werden.

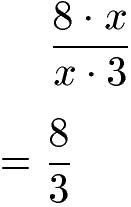
Beispiel 5: Multiplikation und Division

Nach dem Rechnen mit Brüchen - zum Beispiel nach Multiplikationen und Divisionen - kann in einigen Fällen gekürzt werden. In diesem Beispiel berechnen wir zunächst die Klammer und multiplizieren im Anschluss. Danach haben wir mit 40 : 8 einen Bruch, den wir noch kürzen können. Zähler und Nenner können ohne Rest durch 8 geteilt werden.

Anzeigen:

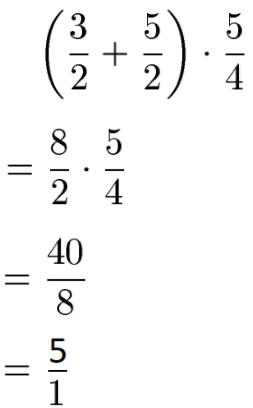
Übungsaufgaben Brüche kürzen

Aufgabe 1: Was ergibt dieser Bruch gekürzt?

2

---

4

• 3 : 4
• 4 : 8
• 10 : 12
• 1 : 2

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Video Brüche kürzen

Fragen mit Antworten Brüche kürzen