Räumliches Koordinatensystem

Mit dem räumlichen Koordinatensystem befassen wir uns hier. Dies sehen wir uns an:

• Eine Erklärung, was ein räumliches Koordinatensystem ist.
• Beispiele wie man Punkte in dieses einträgt.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zum Koordinatensystem.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier das räumlich Koordinatensystem an. Es ist sehr hilfreich wenn ihr bereits das ebene Koordinatensystem kennt und wie man Punkte in dieses einzeichnet. Wer dies noch nicht kann bitte erst in x-y-Koordinatensystem reinsehen.

3D Koordinatensystem Erklärung

In der Mittelstufe lernt man ein x-y-Koordinatensystem kennen. Dieses wird auch als 2D-Koordinatensystem bezeichnet. Man kann mit diesem zum Beispiel die Lage von einem Taschenrechner auf einem Tisch beschreiben. Jedoch kann ein Taschenrechner nicht nur auf einem Tisch liegen sondern auch mit der Hand darüber gehalten werden. Wie gibt man nun an wo sich der Taschenrechner befindet?

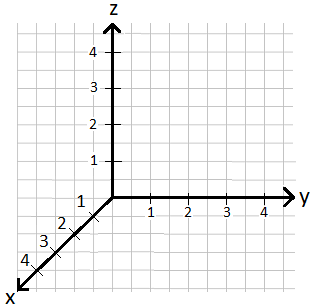
Dazu braucht man eine dritte Angabe: die Höhe. Wir müssen damit unser ebenes Koordinatensystem um eine dritte Ache erweitern. Die nächste Grafik zeigt ein räumliches Koordinatensystem, auch 3D-Koordinatensystem genannt.

Hinweise:

• In der Schule werden die Achsen sehr oft mit x, y und z bezeichnet.
• Dabei zeichnet man oft die x-Achse nach vorne, die y-Achse nach rechts und die z-Achse nach oben.
• Der Ursprung befindet sich an der Stelle an dem sich die Achsen schneiden (x = 0, y = 0 und z = 0).

Anzeige:

Räumliches Koordinatensystem Punkte

Auch in ein räumliches Koordinatensystem lassen sich Punkte einzeichnen. Ein Punkt wird damit nicht nur mit x und y wie in der Ebene angegeben, sondern mit x, y und z. Der Punkt wird damit mit P(x|y|z) definiert.

Beispiel 1: Räumlicher Punkt

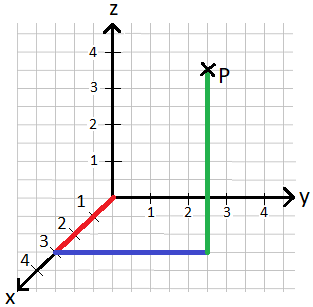
Der Punkt P(3|4|5) soll in ein räumliches Koordinatensystem eingezeichnet werden. Wo liegt dieser?

Lösung:

Der Punkt liegt bei x = 3, y = 4 und z = 5. Wir gehen daher wie folgt vor.

• Wir gehen bis x = 3 auf der x-Achse (rot eingezeichnet).
• Von dort um 4 nach rechts in y-Richtung (blau eingezeichnet).
• Von dieser Stelle 5 nach oben in z-Richtung (grün eingezeichnet).
• Wir sind am Ziel angekommen. Wir markieren die Stelle oder setzen einen Punkt P.

Aufgaben / Übungen räumliches Koordinatensystem

Aufgabe 1: In diesem Abschnitt bekommt ihr Fragen bzw. Übungen zum (räumlichen) Koordinatensystem. Versucht die Fragen selbst zu beantworten, ohne dabei zu schummeln. Wer eine Frage nicht mag kann diese auch überspringen.

• Frage 1: Wie viele Achsen hat ein räumliches Koordinatensystem?

• 4
• 3
• 2
• 1

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Koordinatensystem Video

Fragen mit Antworten 3D-Koordinatensystem