x-y-Koordinatensystem mit Punkte

Was ein x-y-Koordinatensystem ist und wie man Punkte in dieses einträgt, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was ein Koordinatensystem ist.
• Viele Beispiele zum Eintragen von Punkten.
• Aufgaben / Übungen damit ihr dieses Thema selbst üben könnt.
• Ein Video zu diesem Thema.
• Ein Frage- und Antwortbereich zu diesem Bereich.

Hinweis: Wer mit den folgenden Inhalten Verständnisprobleme bekommt, dem fehlen vielleicht einige Vorkenntnisse. Wem die Themen Zahlenstrahl und natürliche Zahlen (1, 2, 3, 4, 5, ...) gar nichts sagen, der kann diese gerne erst noch durch ein Anklicken nachlesen. Ansonsten sehen wir uns jetzt ein einfaches Koordinatensystem an.

Erklärung x-y-Koordinatensystem

Vielleicht erinnert sich der eine oder andere noch an einen Zahlenstrahl. Vereinfacht ausgedrückt handelt es sich dabei um einen "Strich", auf dem in gleichen Abständen weiter gezählt wird. Ein ganz einfacher Zahlenstrahl sieht so aus:

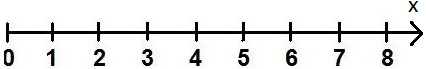
Man kann damit auf einer Linie sagen, ob etwas weiter links (zum Beispiel bei der 2) oder weiter rechts (zum Beispiel bei der 8) sich befindet. Wenn ihr jedoch einen Tisch habt und stellt eine Flasche Wasser auf diesen, dann kann diese nicht nur nach links oder rechts verrückt werden, sondern auch hoch und runter. Daher kann man nun einen zweiten Zahlenstrahl nehmen und diesen von oben nach unten laufen lassen. Die nächste Grafik zeigt euch dies:

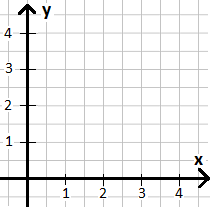
Man bezeichnet dabei den Zahlenstrahl von links nach rechts mit der x-Richtung und den Zahlenstrahl von unten nach oben als y-Richtung. Das Ganze nennt man nun Koordinatensystem. Da die Richtungen (nennt man auch Achsen) mit x und y bezeichnet wurden, nennt man dies auch x-y-Koordinatensystem.

So ein Koordinatensystem dient zum Beispiel dazu die Position von einem Objekt zu beschreiben. Nehmen wir wie weiter oben an, dass es sich dabei um eine Flasche handelt, die auf einem Tisch steht. Deren Boden zeichnen wir einmal mit einem Kreis in das Koordinatensystem ein.

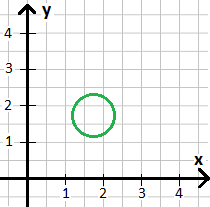
Wir können diese Flasche auf dem Tisch verschieben. Ein bisschen nach oben oder nach rechts zum Beispiel. Aber was passiert, wenn wir sie weit nach links verschieben, oder weit nach unten? Oder sogar beides machen (links und runter)? Dann steht die Flasche links von der y-Achse oder unterhalb der x-Ache. Oder beides.

Aus diesem Grund muss man manchmal - aber nicht immer - das Koordinatensystem mit einem negativen Bereich erweitern. Dazu wird dieses nach links und nach unten erweitert mit Zahlen, die ein Minuszeichen aufweisen. Tipp: Wer noch nie etwas von solchen Zahlen gehört hat, der sieht bitte in den Artikel negative Zahlen rein.

Das x-y-Koordinatensystem wird nun deutlich erweitert. Wir erhalten vier Bereiche, die man auch als Quadranten bezeichnet. Der Punkt an dem die beiden Achsen zusammenlaufen nennt man Ursprung.

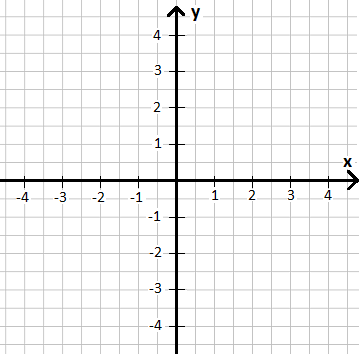
Dieses x-y-Koordinatensystem hat zwei Achsen (x und y). Man bezeichnet dieses daher auch als 2D-Koordinatensystem, denn es werden zwei Dimensionen (links-rechts und oben-unten) dargestellt. Man kann damit auf einem Tisch - also einer Ebene - beschreiben, wo etwas liegt. Daher nennt man dies auch ebenes Koordinatensystem.

Anzeige:

Beispiele x-y-Koordinatensystem mit Punkte

Wo etwas in einem Koordinatensystem liegt, beschreibt man mit Punkten. Genau dies sehen wir uns nun mit einigen Beispielen näher an.

Beispiel 1:

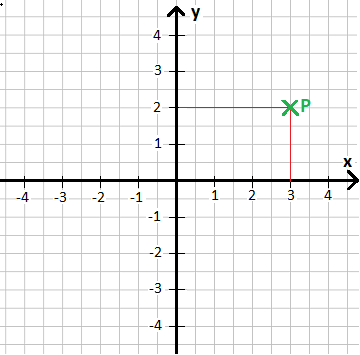
Zeichne den Punkt P(3/2) in ein Koordinatensystem ein.

Lösung:

Bei einem Punkt wird erst der x-Wert, danach der y-Wert angegeben. Der Punkt liegt damit bei x = 3 und y = 2. Wir gehen auf der x-Achse bis zur 3 und von dort nach oben bis wir die Höhe von 2 auf der y-Achse erreichen. An dieser Stelle macht man einen kleinen Punkt oder ein kleines Kreuzchen.

Beispiel 2:

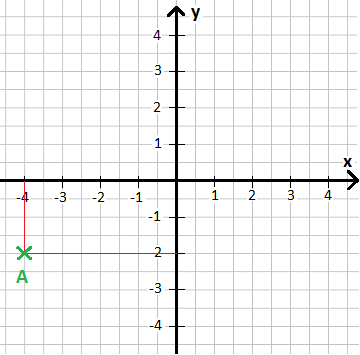
Zeichne den Punk A(-4/-2) in ein x-y-Koordinatensystem ein.

Lösung:

Wir gehen auf der x-Achse nach links, bis wir die -4 erreichen. Danach gehen wir um 2 nach unten, bis wir y = -2 erreichen. Dort setzen wir ein Punkt um A zu markieren.

Beispiel 3:

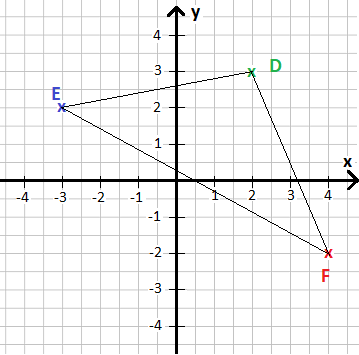
Gib die Koordinaten der der Punkte (Kreuzchen) für D, E und F an.

Lösung:

• Punkt D: Hier geht man auf der x-Achse nach rechts, bis man bei x = 2 landet. Von dort nach oben bis y = 3. Damit ist der Punkt D(2/3).
• Punkt E: Hier geht man auf der x-Achse nach links, bis man bei x = -3 landet. Von dort nach oben bis auf y = 2. Damit ist der Punkt E(-3/2).
• Punkt F: Hier geht man auf der x-Achse nach rechts, bis man bei x = 4 landet. Von dort nach unten bis auf y = -2. Damit ist der Punkt F(4/-2).

Aufgaben / Übungen Koordinatensystem

Aufgabe 1: Der Punkt A hat die Koordinaten A(3/2). Welchem x-Wert entspricht das?

• x = 2
• x = 0
• x = 3
• x = 5

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Koordinatensystem

Fragen und Antworten 2D-Koordinatensystem