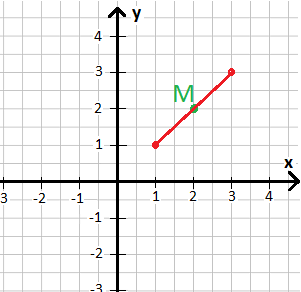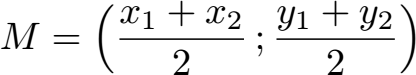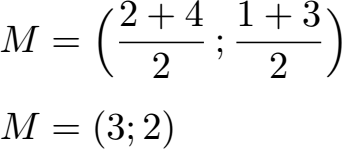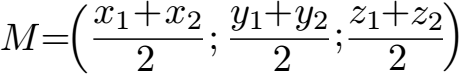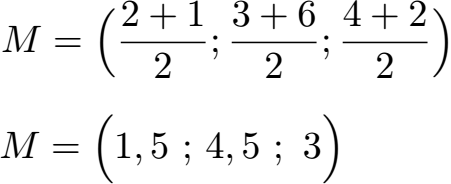Mittelpunkt einer Strecke

Wie man den Mittelpunkt einer Strecke berechnet und wozu man dies braucht, lernt ihr hier. Dies sind die Themen:

• Eine Erklärung, was der Mittelpunkt einer Strecke ist.
• Formeln und Beispiele für die Berechnung in Ebene und Raum.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zum Mittelpunkt einer Strecke.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Euch sollte bereits klar sein, was eine Strecke überhaupt ist. Falls ihr davon keine Ahnung habt, dann werft bitte erst einen Blick in Begriffe der Geometrie. Ansonsten ran an den Streckenmittelpunkt.

Mittelpunkt ebene Strecke

Wo liegt der Mittelpunkt einer Strecke? Um dies zu verstehen werfen wir erst einmal einen Blick auf die nächste Grafik. Hier sieht man ein Koordinatensystem mit einer Strecke. Genau in der Mitte dieser Strecke befindet sich der Mittelpunkt M. Der Mittelpunkt teilt die Strecke in zwei gleichlange Abschnitte.

Möchte man den Mittelpunkt einer Strecke in der Ebene (2D) berechnen verwendet man diese Formel:

Beispiel 1: Mittelpunkt in der Ebene

Wir haben einen Punkt P₁(2;1) und einen Punkt P₂(4;3). Wo befindet sich der Mittelpunkt?

Lösung:

Wir lesen jeweils die x-Werte und y-Werte der Punkte ab und setzen diese in die allgemeine Formel ein. Wir erhalten so rechnerisch den Punkt M(3;2) als Mittelpunkt dieser Strecke,

Anzeige:

Mittelpunkt räumliche Strecke

Strecken können nicht nur in der Ebene, sondern auch im Raum vorkommen. In diesem Fall haben die Punkte jeweils noch eine z-Angabe. Auch unsere Formel zur Berechnung des Mittelpunktes muss erweitert werden.

Beispiel 2: Mittelpunkt räumliche Strecke

Wir haben zwei Punkte mit P1(2;3;4) und P2(1;6;2). Wo liegt der Mittelpunkt?

Lösung:

Wir lesen jeweils x, y und z der beiden Punkte ab und setzen diese in die allgemeine Darstellung ein. Rechnen wir dies aus erhalten wir den Mittelpunkt M bei x = 1,5 sowie y = 4,5 und z = 3.

Aufgaben / Übungen Mittelpunkt einer Strecke

Aufgabe 1:

In diesem Bereich erhaltet ihr die Möglichkeit den Mittelpunkt einer Strecke zu üben.

• Wo liegt der Mittelpunkt einer Strecke die durch die Punkte P₁(1;-2) und P₂(3;4) begrenzt wird?

• M(-1;-2)
• M(3;0)
• M(1;2)
• M(2;1)

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Mittelpunkt Strecke

Fragen mit Antworten zum Streckenmittelpunkt