Primfaktorzerlegung / Primfaktoren

Die Primfaktorzerlegung erklären wir euch hier. Dies sehen wir uns an:

• Eine Erklärung, was Primfaktoren sind und wie man eine Primfaktorzerlegung durchführt.
• Viele Beispiele mit Zahlen.
• Aufgaben / Übungen rund um die Primfaktorzerlegung zum selbst Üben.
• Ein Video zu diesem Thema.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp zum Start: Um die Primfaktorzerlegung selbst durchführen zu können, müsst ihr wissen, was eine Primzahl ist und ihr solltet die Teilbarkeitsregeln kennen. Ich werde beides in Kurzform hier erklären. Wem dies nicht langt schaut bitte in die Hauptartikel zu Primzahlen und Teilbarkeitsregeln.

Erklärung Primfaktorzerlegung

Bei der Primfaktorzerlegung geht es darum eine Zahl in kleine Primzahlen zu zerlegen und diese miteinander zu multiplizieren. Was war noch einmal eine Primzahl? Nun, eine Primzahl ist eine natürlich Zahl, die nur durch sich selbst und durch 1 ohne Rest teilbar ist. Die 1 hat man jedoch ausgenommen. Die ersten Primzahlen lauten 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53.

Teilbarkeit:

Um eine Zahl zerlegen zu können, braucht man noch Wissen zur Teilbarkeit. Ist eine Zahl durch eine andere Zahl ohne Rest teilbar? 6 : 2 = 3. Damit kein Rest. 7 : 2 = 3 Rest 1. Damit haben wir einen Rest.

Wozu braucht man die Primfaktorzerlegung?

Die Zerlegung in Primfaktoren braucht man zum Beispiel...

• ... für die Ermittlung des kgV (kleines gemeinsames Vielfaches)
• ... für die Ermittlung des ggT (größter gemeinsamer Teiler)
• ... in der Bruchrechnung (Hauptnenner und Kürzen)
• ... für Verschlüsselungsverfahren im Datenverkehr

Was sind Primfaktoren?

Darunter versteht man Primzahlen, die miteinander multipliziert werden. Das Wort Faktor kennt hoffentlich jeder noch von Multiplikationen: Erster Faktor mal zweiter Faktor gleich Produkt, zum Beispiel 3 · 4 = 12.

Anzeige:

Beispiele Primfaktorzerlegung

Zerlegen wir einige Zahlen in Primfaktoren. Wir erzeugen damit kleinere Zahlen, die miteinander multipliziert werden. Dazu nehmen wir kleine Primzahlen und versuchen die Ausgangszahl durch diese zu teilen ohne das dabei ein Rest entsteht.

Beispiel 1:

Die Zahl 36 soll in Primfaktoren zerlegt werden. Wie sieht der Rechenweg und das Ergebnis aus?

Lösung:

Zur Erinnerung noch einmal die ersten Primzahlen. Diese waren 2, 3, 5, 7, 11 etc. Wir nehmen jetzt die Ausgangszahl 36 und versuchen diese erst einmal durch 2 zu teilen. Dies geht auch ohne Rest, denn 36 : 2 = 18. Damit sieht die Primfaktorzerlegung bis jetzt so aus:

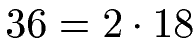
Jetzt prüfen wir, ob eine weitere Zerlegung möglich ist. Dazu sehen wir uns die 18 an und prüfen, ob diese durch 2 teilbar ist. Dies geht auch, denn 18 : 2 = 9.

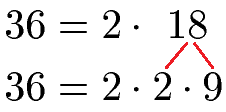
Können wir die 9 noch zerlegen? Versuchen wir es wieder mit der 2. Dann erhalten wir 9 : 2 = 4 Rest 1. Wir haben einen Rest. Daher versuchen wir es mit der nächsten Primzahl, welche die 3 ist. Mit 9 : 3 = 3 klappt dies auch ohne Rest. Wir haben damit auf der rechten Seite der Gleichung nur Primfaktoren. Damit sind wir fertig. Die komplette Zerlegung in Primfaktoren sieht damit so aus:

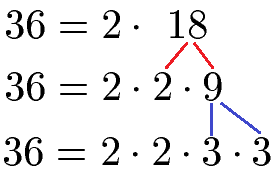
Beispiel 2:

Die Zahl 450 soll in Primfaktoren zerlegt werden.

Lösung:

Wir nehmen die 450 und versuchen erst einmal durch 2 zu teilen. Dies geht auch, dann die 450 endet auf die Zahl 0 und ist daher durch 2 ohne Rest teilbar. Mit 450 : 2 = 225 machen wir den ersten Schritt.

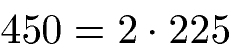
Können wir die 225 zerlegen? Mit einer 2 sicher nicht, dann 225 endet auf eine 5 und ist daher nicht ohne Rest durch 2 teilbar. Daher versuchen wir es mit der nächsten Primzahl, der 3. Dies geht, denn die Quersumme von 225 ist 2 + 2 + 5 = 9. Und 9 ist ohne Rest durch 3 teilbar. Wir können daher die 225 in 3 · 75 zerlegen.

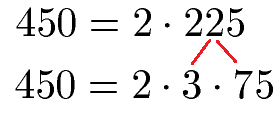
Die 75 können wir nicht durch 2 teilen ohne Rest. Durch 3 hingegen schon, da 75 = 3 · 25.

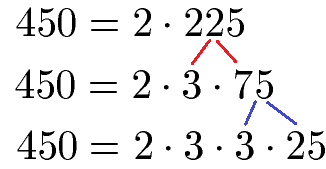
Die 25 können wir weder durch 2 noch durch 3 ohne Rest teilen. Allerdings durch die nächste Primzahl - die 5 - geht es. Wir erhalten damit 25 = 5 · 5. Damit ist die Zerlegung in Primfaktoren komplett. Die fertige Berechnung sieht so aus:

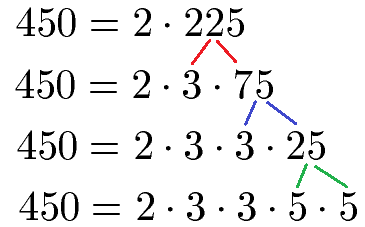
Beispiel 3 mit Primfaktor Baum:

Werden die Zahlen größer (weit über 100 oder gar über 1000) kann man einen Baum verwenden um die Zahl in ihre Primfaktoren zu zerlegen. Gezeigt werden soll dies einmal an der Zahl 700. Zunächst der komplette Baum mit Rechenweg, im Anschluss wird dieser erklärt.

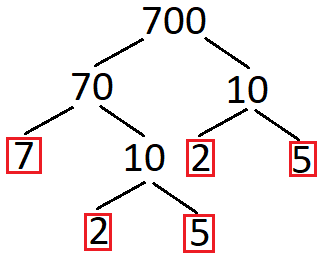
Im Prinzip nehmen wir die Ausgangszahl und versuchen stets kleinere Multiplikationen aufzubauen. Für den Start 700 = 70 · 10. Diese zerlegen wir immer weiter bis wir jeweils nur noch Primzahlen haben. Erreichen wir eine Primzahl, kreisen wir diese jeweils rot ein. Daraus ergibt sich dann:

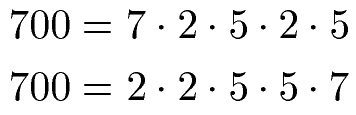
Aufgaben / Übungen Primfaktoren

Aufgabe 1: Bevor es Übungen zur Primfaktorzerlegung gibt schnell ein Fragen zu den Grundlagen. Welche der folgenden Zahlen ist ohne Rest durch 2 teilbar? 3, 5, 6 oder 9?

• 9
• 6
• 5
• 3

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Videos Primfaktorzerlegung

Fragen mit Antworten Primfaktorzerlegung