Gedämpfte Schwingung

Mit der gedämpften Schwingung befassen wir uns in diesem Artikel. Folgende Inhalte werden angeboten:

• Zunächst eine Erklärung, was eine gedämpfte Schwingung überhaupt ist.
• Im Anschluss Beispiele mit Zahlen und Einheiten zum besseren Verständnis.
• Ihr bekommt Aufgaben / Übungen bzw. Fragen zu diesem Thema um euer Wissen zu kontrollieren.
• Ein Video soll ebenfalls euch die gedämpfte Schwingung näher bringen
• Ein Frage- und Antwortbereich rundet den Artikel am Ende ab.

Wir befassen uns gleich mit der gedämpften Schwingung. Die Inhalte sind dabei nicht ganz einfach. Wer Probleme mit dem Verständnis hat, dem fehlen aber oft einige wichtige Vorkenntnisse. In diesem Fall bitte folgende Inhalte noch lernen: Funktionen zeichnen, E-Funktion und harmonische Schwingungen. Ihr solltet auch Begriffe wie Amplitude und Frequenz sowie Kreisfrequenz kennen.

Erklärung gedämpfte Schwingung

Eine sinusförmige, harmonische Schwingung kennt ihn nun also hoffentlich. Bei dieser ist die Amplitude durchgehend gleich. Bei einer gedämpften Schwingung ist das nicht der Fall. Ist hier die Dampfung nicht zu extrem, erhalten wir einen Schwingfall. Dabei ist die Amplitude nicht konstant, sondern nimmt mit der Zeit (exponentiell) ab.

Beispiel: Ein Beispiel für eine gedämpfte Schwingung wäre ein reales Fadenpendel (Was ist ein Fandenpendel?). Wegen der (Luft-)Reibung schwingt dieses mit der Zeit immer weniger, sprich die Amplitude wird kleiner. Wartet man sehr lange, sieht man irgendwann gar keine Bewegung mehr. Die mechanische Energie des Fadenpendels verringert sich mit der Zeit.

Auch mathematisch kann man solch einen gedämpften Schwingungsfall beschreiben:

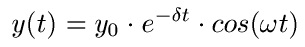
Der Anfang davon, also y_o · e-^δt, ist die Amplitude. Und diese nimmt mit der Zeit ab. Das Delta "δ" wird als Abklingzeitkonstante bezeichnet. Sie gibt an, wie stark die Dämpfung ist.

Anzeige:

Beispiel gedämpfte Schwingung

Wie sieht nun so eine gedämpfte Schwingung aus? Aus diesem Grund machen wir ein Beispiel. Dazu nehmen wir die allgemeine Gleichung von oben:

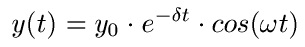
Und in diese setzen wir nun einmal einige Beispielwerte ein und zeichnen dann:

Beispiel 1:

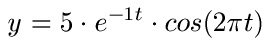
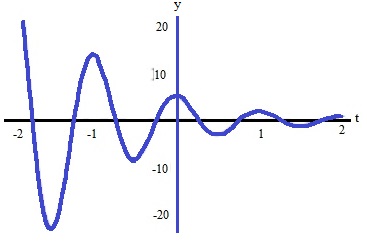
Aufgaben / Übungen gedämpfte Schwingungen

Aufgabe 1: In diesem Bereich bieten wir euch Aufgaben / Fragen zur gedämpften Schwingung. Wer eine Frage / Aufgabe nicht mag, der kann auf "Überspringen" klicken. Zur ersten Frage: Was ist typisch für eine gedämpfte Schwingung?

• Konstante Amplitude
• Keine Amplitude
• Steigende Amplitude
• Abnehmende Amplitude

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Gedämpfte Schwingung Video

Fragen und Antworten gedämpfte Schwingung