ABC-Formel: Beispiele und Erklärung

Was die ABC-Formel ist und wie man sie benutzt, lernt ihr hier. Folgende Inhalte werden angeboten:

• Eine Erklärung, was die ABC-Formel ist und wozu man sie braucht.
• Beispiele zum Anwenden der ABC-Formel.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu diesem Thema
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Hinweis: Die ABC-Formel wird manchmal auch Mitternachtsformel genannt. Wer diese Formel nicht mag, kann die Aufgaben auch mit der PQ-Formel lösen.

Erklärung: ABC-Formel

Die ABC-Formel verwendet man in der Mathematik dazu quadratische Gleichungen bzw. quadratische Funktionen zu lösen. Eine quadratische Gleichung bzw. Funktion sieht so aus:

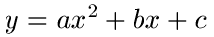
Hier noch einige Beispiele für quadratische Funktionen / Gleichungen:

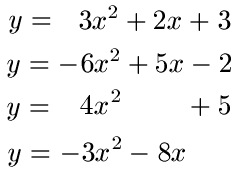
Mit der ABC-Formel kann man Nullstellen berechnen. Nullstellen sind die Stellen, bei denen y = 0 ist. Es sind damit die Stellen, an denen der Verlauf einer Funktion die x-Achse schneidet. Die nächste Grafik zeigt ein Beispiel. Die Nullstellen sind dabei rot eingekreist.

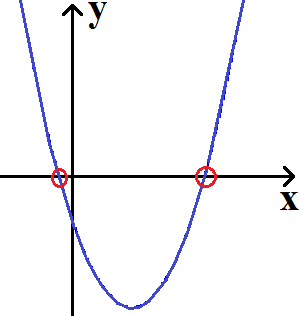
An den roten eingekreisten Stellen - also den Nullstellen - ist y = 0. Dies nutzen wir bei der Berechnung aus. Haben wir eine quadratische Funktion oder Gleichung und suchen bei dieser die Nullstellen, dann müssen wir diese in eine Form mit = 0 bringen. Danach kann die ABC-Formel verwendet werden, um die Nullstellen zu berechnen. Die allgemeine Form:

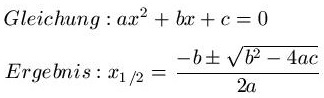
Ob die quadratische Funktion eine, zwei oder gar keine Nullstellen hat, hängt von dem ab, was unter der Wurzel steht (Diskriminante).

Anzeige:

Beispiele ABC-Formel

Sehen wir uns einige Beispiele zur ABC Formel an. Dabei gehen wir die Frage an: Wie kann man die ABC-Formel einsetzen?

Beispiel 1: ABC-Formel mit zwei Nullstellen

Berechnet werden sollen die Nullstellen der Gleichung 3x² + 9x + 5 = -1. Wo liegen diese?

Lösung:

Wir formen die Gleichung zunächst so um, dass wir ein = 0 erhalten. Danach lesen wir a, b und c ab. Dies wurde farblich markiert. Wir können dies im Anschluss in die ABC-Formel einsetzen. Wir rechnen zunächst alles unter der Wurzel aus und erhalten eine 9. Die Wurzel aus 9 ziehen wir und erhalten 3. Als nächstes können wir beide Nullstellen berechnen. Dabei nehmen wir einmal ein Plus vor der 3 und einmal ein Minus vor der 3.

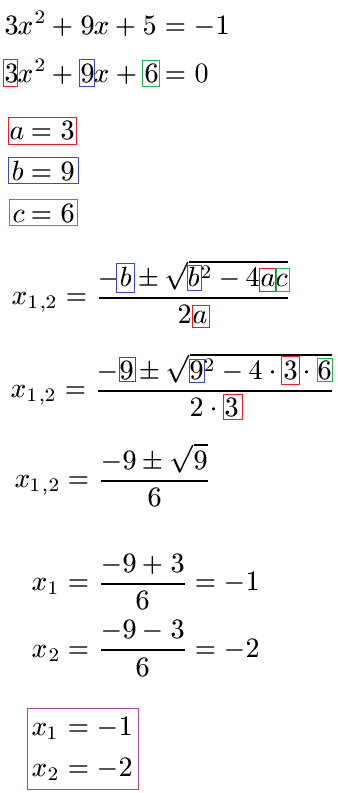
Wir erhalten damit die Nullstellen bei x = -1 und x = -2.

Beispiel 2: ABC-Formel ohne Nullstellen

Im zweiten Beispiel haben wir die Gleichung 2x² + 3x + 30 = 0. Wo liegen die Nullstellen?

Lösung:

Díe Gleichung ist bereits in der Form mit = 0. Aus diesem Grund müssen wir hier keine Umformung durchführen. Aus der Gleichung können wird direkt a = 2, b = 3 und c = 30 ablesen. Dies setzen wir in die Lösungsformel ein. Dabei entsteht ein "Problem". Die Diskriminante - also das was unter der Wurzel steht - wird negativ. In der Schule lernt man, dass man aus negativen Zahlen keine Wurzel ziehen kann. Aus diesem Grund ist die Berechnung an dieser Stelle fertig und es gibt keine Nullstellen.

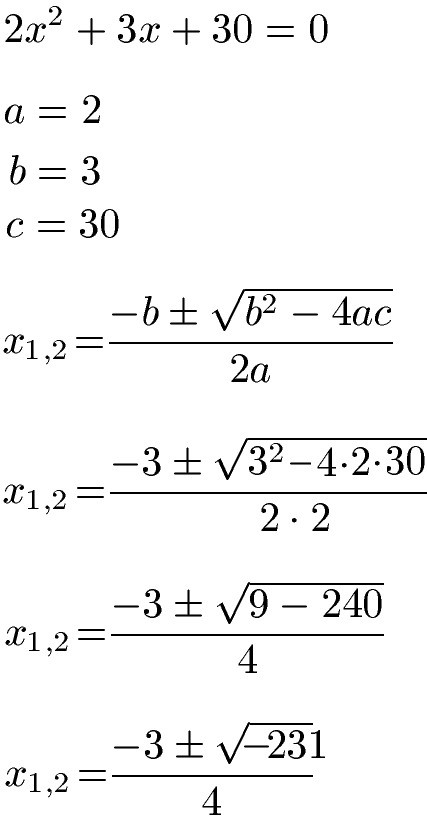
Beispiel 3: Doppelte Nullstelle

Gegeben sei die Gleichung x² + 4x + 4 = 0. Berechne mit der ABC-Formel die Nullstellen.

Lösung:

Wir können direkt a = 1, b = 4 und c = 4 ablesen. Die setzen wir in die Lösungsgleichung ein. Unter der Wurzel entsteht dabei eine 0. Dies führt bei der Berechnung mit + und mit - vor der Null dazu, dass wir zwei Mal die selbe Zahl für x erhalten. Bei x = -2 liegt damit eine doppelte Nullstelle vor.

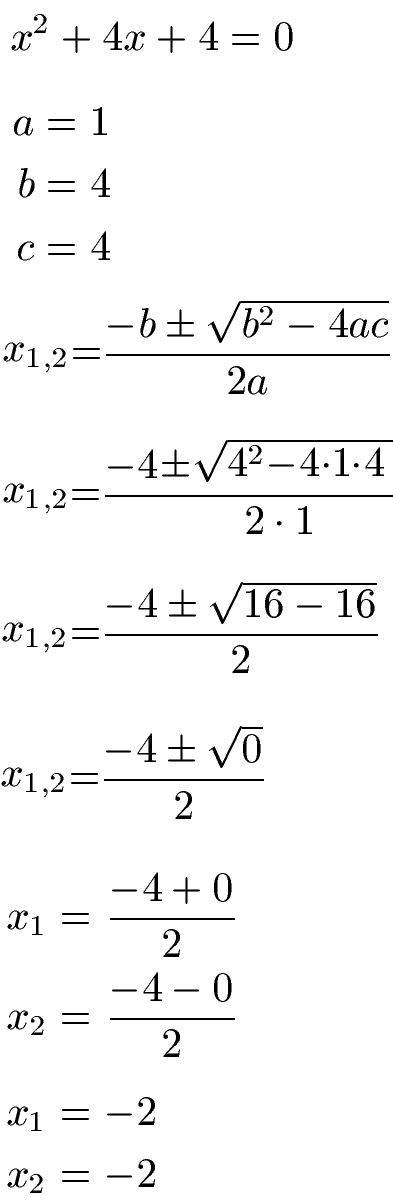
Aufgaben / Übungen zur ABC-Formel

Aufgabe 1: Bevor wir rechnen kurz ein paar (einfache) Fragen. Was kann man mit der ABC-Formel lösen?

• Kubische Gleichungen
• Lineare Gleichungen
• Gleichungen 5. Grades
• Quadratische Gleichungen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video ABC-Formel

Fragen mit Antworten zur ABC-Formel