Brüche ordnen / sortieren
Geschrieben von: Dennis RudolphDienstag, 20. April 2021 um 17:08 Uhr
Wie man Brüche ordnen bzw. sortieren kann, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, wie man Brüche auf einen Hauptnenner bringt und danach ordnet.
- Viele Beispiele zum Sortieren von Brüchen.
- Aufgaben / Übungen damit ihr das Thema selbst üben könnt.
- Videos zur Bruchrechnung.
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Hinweis: Wenn ihr nicht wisst, was ein Bruch mit Zähler und Nenner ist, werft bitte erst einmal einen Blick in den Hauptartikel Bruchrechnen. Ansonsten sehen wir uns nun an, wie man Brüche ordnen bzw. sortieren kann.
Erklärung Brüche ordnen
Welcher Bruch ist größer? Welcher Bruch ist kleiner? Solche Fragen stellen Lehrer und Lehrerinnen im Mathematik-Unterricht. Dabei sollen oftmals Brüche miteinander verglichen werden und im Anschluss diese der Größe nach geordnet werden. Dies sollt ihr hier nun lernen.
Beginnen wir mit dem einfachsten Fall. Bei diesem haben wir gleichnamige Brüche. Darunter versteht man Brüche, welche alle den gleichen Nenner haben. In diesem Fall ist der Bruch mit dem kleinsten Zähler auch der kleinste Bruch.
Beispiel 1:
Mehrere Brüche sollen der Größe nach geordnet werden, beginnend mit dem kleinsten Bruch.
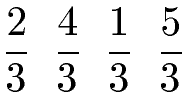
Lösung:
Alle Brüche haben die 3 als Nenner. Daher müssen wir nur einen Blick auf die Zähler werfen. Je kleiner der Zähler ist, desto kleiner ist auch der Bruch. Wir schreiben damit die kleinste Zahl nach links.
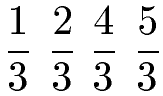
Fehlt uns noch das Zeichen für den Vergleich. Dabei gibt es kleiner (<), größer (>) und gleich (=). Die kleinere Zahl steht links, daher passt das "<" zwischen den Zahlen.
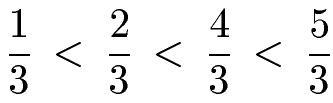
Beispiel 2:
Es gibt noch einen weiteren Fall, indem man sofort und ohne zu rechnen die Brüche sortieren kann. In diesem Fall sind alle Zähler gleich und alle Nenner verschieden. Ordne die nächsten Brüche der Größe nach, beginnend mit der größten Zahl.
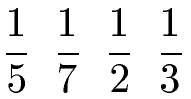
Lösung:
Haben zwei Brüche den gleichen Zähler, so ist der Bruch mit dem kleineren Nenner der größere Bruch. Wir schreiben damit den größten Bruch (1/2) ganz links und sortieren dann von links nach rechts, beginnend mit dem größten Bruch bis hin zum kleinsten Bruch. Das mathematische Zeichen für größer ist das ">".
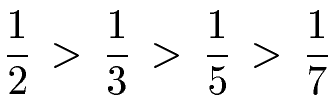
Regeln Brüche ordnen / sortieren:
- Haben Brüche den gleichen Nenner, dann ist der Bruch mit dem kleinsten Zähler auch der kleinste Bruch.
- Haben Brüche den gleichen Zähler, so ist der Bruch mit dem kleinsten Nenner der größte Bruch.
- Haben Brüche verschiedene Zähler und Nenner, so bringt man die Brüche auf einen gemeinsamen Nenner und ordnet im Anschluss.
Die letzte der drei Regeln sehen wir uns im nächsten Abschnitt an.
Anzeigen:
Beispiele Brüche sortieren
Wenden wir uns etwas schwierigeren Aufgaben zu. Dabei haben wir verschiedene Zähler und Nenner. Um diese Brüche ordnen zu können, bringen wir diese zunächst auf einen gemeinsamen Nenner. Im Anschluss können wir sortieren.
Beispiel 3:
Wir haben zwei Brüche. Ordne diese beiden Brüche der Größe nach, beginnend mit der kleineren Zahl.
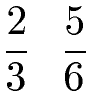
Lösung:
Wir haben die Nenner 3 und 6. Um den linken Bruch auf den Nenner 6 zu bringen, müssen wir den Nenner mit 2 multiplizieren. Dies machen wir auch im Zähler. Im Zähler haben wir damit 2 · 2 = 4 und im Nenner 3 · 2 = 6. Aus dem ersten Bruch mit 2/3 wird damit 4/6. Diesen können wir vergleichen und sehen, das 4/6 kleiner als 5/6 ist.
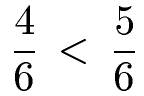
Beispiel 4:
Machen wir mal etwas schwierigeres. Wir haben drei Brüche, welche der Größe nach sortiert werden sollen, beginnend mit dem größten Bruch.
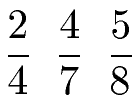
Lösung:
Wir haben mit 4, 7 und 8 verschiedene Nenner. Auf den ersten Blick einfach einen gemeinsamen Nenner zu finden ist nicht so einfach. Wir müssen diesen also suchen. Wie macht man das? Antwort: Mit dem kleinsten gemeinsamen Vielfachen. Dies ist ganz einfach. Wir schreiben von 4, 7 und 8 die Vielfachen auf und suchen dann die kleinste gemeinsame Zahl unter den Vielfachen raus.
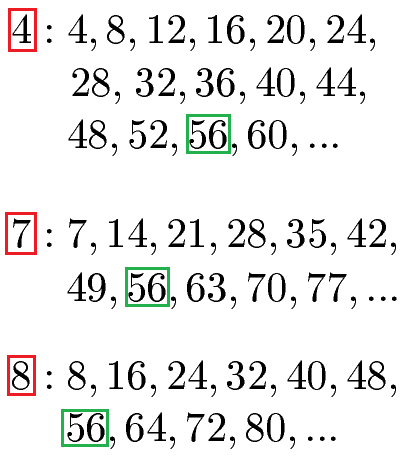
Das kleinste gemeinsame Vielfache ist damit 56. Wir müssen jetzt ausrechnen mit welchen Zahlen wir die Brüche erweitern müssen. Dazu nehmen wir die 56 und teilen durch 4, 7 und 8.
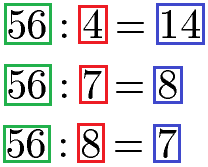
Jetzt nehmen wir die drei Brüche vom Beginn und erweitern mit 14, 8 und 7.
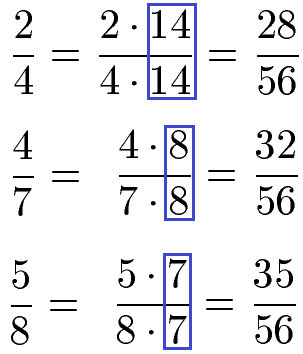
Jetzt haben wir 3 Brüche mit gleichem Nenner. Jetzt sortieren wir den größten Bruch nach vorne und den kleinsten Bruch nach hinten. Je größer der Zähler, desto größter der Bruch.
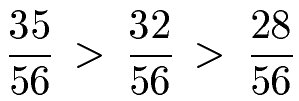
Aufgaben / Übungen Brüche sortieren
Anzeigen:Video Brüche ordnen
Sortieren von Brüchen
In diesem Video geht es um das Sortieren bzw. Ordnen von Brüchen:
- Aufbau eines Bruchs.
- Sortieren bei gleichen Zählern.
- Sortieren bei gleichnen Nennern.
- Brüche auf gleichen Nenner bringen.
- Beispiele zum Sortieren.
- Erklärungen zum Ordnen.
Nächstes Video »
Fragen mit Antworten Brüche ordnen / sortieren
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zum Sortieren bzw. Ordnen von Brüchen an.
F: Kann man Brüche ordnen ohne sie gleichnamig zu machen?
A: Ja, kann man. Eine Möglichkeit hatten wir oben in Beispiel 2, bei denen die Zähler gleich waren. Dann kann man direkt über die Nenner sehen, welche Zahl größer oder kleiner ist. Eine weitere Möglichkeit wäre die Brüche "auszurechnen", sprich Dezimalzahlen (Kommazahlen) daraus zu machen und diese dann zu vergleichen. Eine weitere Möglichkeit ist ein sehr gutes Mathematik-Verständnis, bei der man im Kopf eine Vorstellung hat, wie groß ein Bruch ist um diese im Kopf miteinander vergleichen zu können.
F: Wann wird das Sortieren bzw. Ordnen von Brüchen in der Schule gemacht?
A: Frühstens in der 5. Klasse steht das Thema auf dem Plan, spätestens in der 6. Klasse. Die Bruchrechnung selbst wird jedoch auch in der 7. Klasse und danach behandelt.
F: Kann man Brüche auf einem Zahlenstrahl ordnen?
A: Selbstverständlich kann man nicht nur natürliche oder ganze Zahlen, sondern auch Brüche auf einem Zahlenstrahl darstellen. Wie dies funktioniert, seht ihr unter Zahlenstrahl Brüche.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
