Dreieck Flächeninhalt ▷ Fläche berechnen
Geschrieben von: Dennis RudolphDienstag, 10. Mai 2022 um 17:45 Uhr
Wie man von einem Dreieck die Fläche (Flächeninhalt) berechnet, lernst du hier. Dies sehen wir uns an:
- Eine Erklärung, wie man die Fläche von einem Dreieck berechnet.
- Beispiele zum Einsatz der Formel mit Zahlen und Einheiten.
- Aufgaben / Übungen damit ihr das Berechnen vom Flächeninhalt selbst üben könnt.
- Ein Video zum Dreieck.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Wir sehen uns gleich das Dreieck an. Zum Rechnen damit solltet ihr Wissen was Meter und Zentimeter sind. Falls nicht bitte in die Längeneinheiten reinsehen. Die Formeln beinhalten Variablen (Buchstaben). Wer noch nicht weiß, was das ist, sieht bitte in Variablen rein.
Flächeninhalt rechtwinkliges Dreieck
Der Flächeninhalt eines Dreiecks ist halb so groß wie der Flächeninhalt des entsprechenden Rechtecks. Bei einem Rechteck wird die Fläche mit Länge mal Breite berechnet. Für das Dreieck muss diese im Anschluss halbiert werden. Die nächste Grafik verdeutlicht dies optisch.
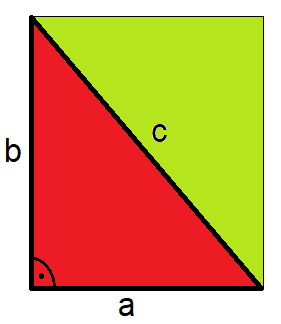
Die Formel für den Flächeninhalt eines Dreiecks ist damit Länge mal Breite geteilt durch 2.
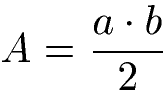
Beispiel Flächeninhalt rechtwinkliges Dreieck:
Um den Flächeninhalt von einem Dreieck zu berechnen, werden für die Seiten die Längenangaben für "a" und "b" eingesetzt. Ist die Länge der Seite "a" 4 cm und die Länge der Seite "b" 5 Zentimeter kann dies in die Formel eingesetzt und die Fläche berechnet werden.
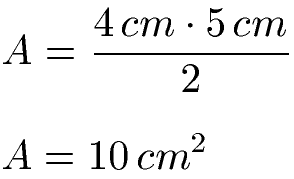
Beachte bei der Berechnung das Zentimeter (cm) mal Zentimeter (cm) zu Quadratzentimeter (cm2) wird.
Anzeige:
Anzeigen:
Flächeninhalt Dreieck mit Formel
Der Flächeninhalt eines beliebigen Dreiecks kann aus Grundseite mal Höhe geteilt durch 2 berechnet werden. Auf der Grundseite (c) steht dabei die Höhe (h) welche die maximal Höhe im Dreieck darstellt und in der Spitze endet.
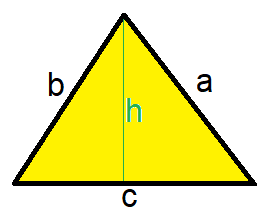
In der Formel für den Flächeninhalt "A" wird die Grundseite "c" mit der Höhe "h" multipliziert. Das Ergebnis wird durch 2 geteilt. Die Formel ähnelt dabei stark der Berechnung eines rechtwinkligen Dreiecks.
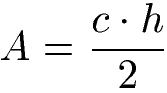
Beispiel Dreieck Flächeninhalt:
Die Grundseite eines Dreiecks sei 8 Zentimeter lang. Die Höhe wird mit 6 Zentimeter gemessen. Berechne die Fläche des Dreiecks. Zur Lösung setzen wir c = 8 cm und h = 6 cm in die Formel ein.
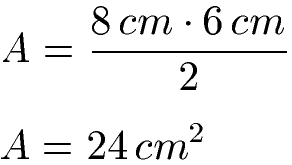
Das Dreieck hat einen Flächeninhalt von 24 Quadratzentimetern.
Flächeninhalt gleichschenkliges Dreieck
Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Schenkeln. Beide Schenkel haben dadurch die Seitenlänge "a". Die Grundseite des Dreiecks wird als "c" bezeichnet.
Der Flächeninhalt eines gleichschenkligen Dreiecks kann nach der folgenden Formel berechnet werden.
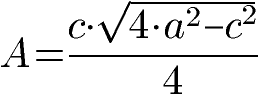
Als Beispiel dient ein gleichschenkliges Dreieck mit der Schenkellänge von 3 Metern und einer Grundseite von 4 Metern. Wie groß ist die Fläche des Dreiecks? Zur Lösung setzen wir c = 4 m und a = 3 m in die Gleichung ein. Beachte dabei zuerst die Potenz unter der Wurzel zu rechnen, danach Punkt vor Strich.
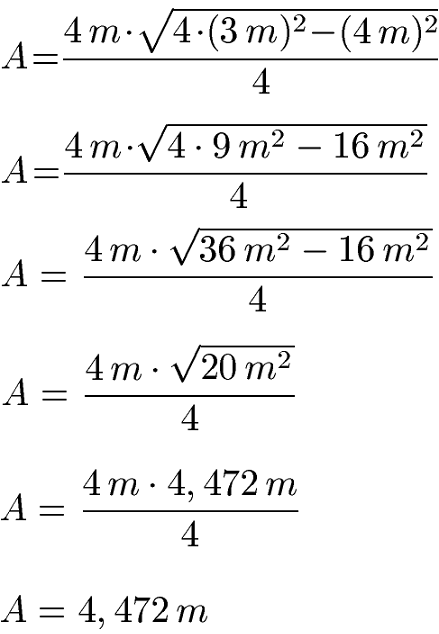
Wir erhalten einen Flächeninhalt von 4,472 Quadratmetern für das gleichschenklige Dreieck.
Anzeigen:
Flächeninhalt gleichseitiges Dreieck
Ein gleichseitiges Dreieck ist ein Dreieck mit drei gleich langen Seiten. Die Seitenlänge für alle drei Seiten wird mit "a" bezeichnet.
Der Flächeninhalt eines gleichseitigen Dreiecks lässt sich alleine mit der Länge "a" berechnen. Die Formel lautet:
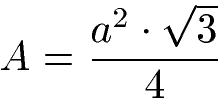
Als Beispiel dient ein gleichseitiges Dreieck mit der Seitenlänge von 2 Metern. Beachte bei der Berechnung, dass die Potenz (Hoch 2) sich nicht nur auf die Zahl 2, sondern auf 2 m bezieht. Daher muss sowohl die 2 als auch m quadriert werden.
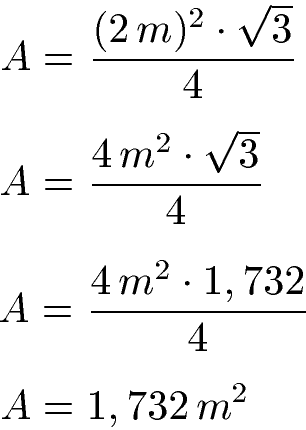
Das gleichseitige Dreieck mit Seitenlänge 2 Meter hat einen Flächeninhalt von 1,732 Quadratmetern.
Aufgaben / Übungen Dreieck Fläche
Video Fläche Dreieck
Formel und Beispiel
In diesem Video geht es um die Berechnung der Fläche eines Dreiecks. Dabei wird zunächst kurz auf die Bezeichnung der Seiten eingegangen bzw. der Eckpunkte. Die Formel für eine Dreieck-Fläche wird gezeigt und wie man in diese entsprechende Angaben einsetzt. Man muss jedoch sehr aufpassen, dass alle Angaben in der selben Einheit eingesetzt werden. Dieses Video stammt von Youtube.com.
Fragen mit Antworten: Fläche Dreieck
In diesem Abschnitt werden typische Fragen mit Antworten zum Flächeninhalt eines Dreiecks vorgestellt.
Wie kann man die Höhe in einem Dreieck berechnen?
Die Höhe in einem Dreieck lässt sich mit einem Winkel und einer Seitenlänge berechnen.
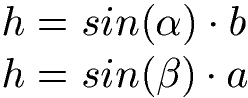
Wie berechnet man die Fläche eines Dreiecks aus dem Umfang?
Der Flächeninhalt eines Dreiecks lässt sich mit dem Umfang und den Seitenlängen berechnen. Dazu wird die Hilfsvariable "s" berechnet, welche der halbierte Umfang ist. Damit wird in eine etwas schwierigere Gleichung mit s, a, b und c eingesetzt.
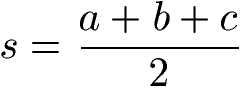
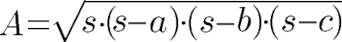
Was muss ich bei den Einheiten beachten?
In die Formel bzw. Formeln setzt man nicht nur Zahlen, sondern auch Einheiten ein. In diesem Artikel wurden die Längeneinheiten Zentimeter und Meter benutzt. Bei Formeln ist es sehr wichtig, dass man alle Angaben in der selben Einheit einsetzt. So kann man zum Beispiel alles in Meter oder alles in Zentimeter einsetzen. Gemischt darf man dies jedoch nicht tun, sonst kommt bei der Berechnung ein fehlerhaftes Ergebnis raus. Dies bedeutet: Am Anfang alles auf eine Einheit umrechnen.
Wann wird dieses Thema in der Schule behandelt?
Die Flächenberechnung wird in der 5. Klasse und 6. Klasse der Schule in Mathematik behandelt. Zunächst geht es dabei um sehr einfache Dinge wie die Fläche von einem Rechteck. Bald darauf folgt jedoch auch die Fläche von einem Dreieck (oft in der 6. Klasse).
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
