Einmaleins online lernen und üben kostenlos

Mit dem Einmaleins samt Erklärungen und Aufgaben zum Selbst üben befassen wir uns in diesem Artikel. Wer gleich üben möchte kann gleich die Aufgaben / Übungen aufrufen. Ansonsten werden folgende Inhalte angeboten:

• Erklärungen zum Einmaleins und wie man Multiplikationen durchführt.
• Beispiele zum Einmaleins mit Zahlen ausführlich vorgerechnet und erklärt.
• Aufgaben bzw. Übungen zum Einmaleins damit ihr selbst trainieren könnt.
• Ein Video zur Multiplikation bzw. Einmaleins Aufgaben
• Ein Frage- und Antwortbereich zu diesem Thema.

Wir befassen uns gleich mit dem Einmaleins, sprich mit Multiplikationen von Zahlen. Dabei sehen wir uns erst einmal das kleine Einmaleins von 1 · 1 = 1 bis 10 · 10 = 100 an. In einem Folgeartikel - verlinke ich hier sobald verfügbar - sehen wir uns noch das große Einmaleins bis 20 · 20 = 400 an. Wie auch immer: Um das Einmaleins zu verstehen, sind ein paar Grundlagen der Mathematik sinnvoll. Zunächst solltet ihr das Rechnen bis 100: Addition und Subtraktion sowie Multiplikation / Malnehmen 2. Klasse drauf haben.

Erklärung und Tabelle Einmaleins

Was versteht man unter dem Einmaleins? Nun, unter dem 1x1 bzw. 1mal1 versteht man alle Produkte, die sich aus der Kombination zweier natürlicher Zahlen von 1 bis 10 ergeben. Oft stellt man dies in einer Tabelle dar und man rechnet dazu alle Kombinationen durch. Wir werfen nun einen kurzen Blick auf die Tabelle. Im Anschluss wird genauer darauf eingegangen, wie man auf diese Tabelle kommt.

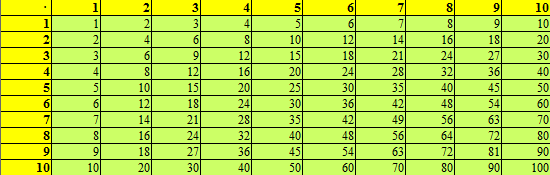
Wie kommt man nun auf die Tabelle zum 1mal1? Nun, dazu muss man im Prinzip alle Kombinationen von 1 · 1 bis 10 · 10 ausrechnen. Wer fit in der Multiplikation kleiner Zahlen ist, der kann die Ergebnisse auch direkt hinschreiben. Für alle anderen gleich noch eine Erklärung, wie man auf die Tabelle kommt. Dazu rechnet man alle Aufgaben einzeln durch. Hier mal ein kleiner Auszug aus den Rechnungen:

• 4 · 3 = 12
• da 3 + 3 + 3 + 3 = 12

• 5 · 10 = 50
• da 10 + 10 + 10 + 10 + 10 = 50

• 7 · 3 = 21
• da 3 + 3 + 3 + 3 + 3 + 3 + 3 = 21

Rechnet man dies Stück für Stück durch, erhält man ganze Reihen an Zahlen um diese Tabelle zu bilden. Wir haben also die 2er-Reihe, 3er-Reihe usw. bis zur 10er-Reihe. Dies sieht dann so aus:

Für 1er, 2er und 3er Reihe:

Für 4er, 5er und 6er Reihe:

Für 7er, 8er, 9er und 10er Reihe:

Soweit zu den Reihen für das Einmaleins (1mal1 oder 1x1 oder wie auch immer man es noch nennen mag). Im nächsten Abschnitt sehen wir uns Beispiele zum Berechnen von Aufgaben zum Einmaleins an.

Anzeige:

Beispiele Einmaleins / 1mal1 / 1x1

Sehen wir uns nun eine Reihe an Beispielen an, so wie diese oft für das Einmaleins in der Schule gestellt werden. Die Beispiele werden ausführlich vorgerechnet. Wer bereits fit in der Multiplikation ist, der kann die Lösung der Aufgabe auch direkt hinschreiben.

Beispiel 1:

• 5 · 4 = ___
• 4 + 4 + 4 + 4 + 4 = 20
• 5 · 4 = 20

Beispiel 2:

• 3 · 8 = ___
• 8 + 8 + 8 = 24
• 3 · 8 = 24

Beispiel 3:

• 6 · 7 = ___
• 7 + 7 + 7 + 7 + 7 + 7 = 42
• 6 · 7 = 42

Beispiel 4:

• 2 · 4 = ___
• 4 + 4 = 8
• 2 · 4 = 8

Einmaleins Aufgaben + Übungen

Aufgabe 1: Was ergibt 2 · 4 = ___ ?

• 4
• 10
• 8
• 6

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.

Anzeigen:

Einmaleins Videos

Einmaleins: Fragen und Antworten