Ganze Zahlen
Geschrieben von: Dennis RudolphSonntag, 27. Juni 2021 um 15:38 Uhr
Was ganze Zahlen sind (und was nicht) und wie man mit diesen rechnet, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, was ganze Zahlen sind.
- Viele Beispiele zum Umgang mit ganzen Zahlen.
- Aufgaben / Übungen damit ihr diesen Zahlentyp selbst üben könnt.
- Ein Video zu diesem Thema.
- Ein Frage- und Antwortbereich zu ganzen Zahlen.
Wir sehen uns gleich an, was ganze Zahlen sind. Ein Teil der ganzen Zahl sind die natürlichen Zahlen. Wer zu diesen noch etwas lernen möchte, der kann auch erst noch einen Blick auf die natürlichen Zahlen werfen.
Erklärung ganze Zahlen
Was sind ganze Zahlen? Das Gegenteil von "kaputten" Zahlen könnte man meinen. Im Prinzip ist dem sogar so. Denn bei den ganzen Zahlen handelt es sich um all die Zahlen, welche "ganz" sind und keine Anteile hinter einem Komma haben. Dies sind zunächst die natürlichen Zahlen inklusive der Null (0, 1, 2, 3, 4, 5, 6 usw.) und genau diese Zahlen noch mit einem Minuszeichen davor (-1, -2, -3, -4, -5, -6 usw.)
Definition und Eigenschaften ganzen Zahlen:
- Zu den ganzen Zahlen gehören alle natürlichen Zahlen, inklusive der Null. Dies sind:
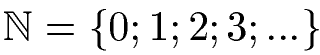
- Ebenfalls zu den ganzen Zahlen gehören genau diese Zahlen noch mit einem Minuszeichen davor
Man fasst die ganzen Zahlen mit dem Buchstaben Z zusammen, bei dem ein Doppelstrich eingesetzt wird.
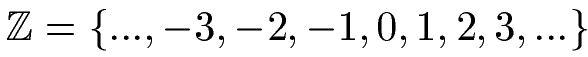
Beispiel 1:
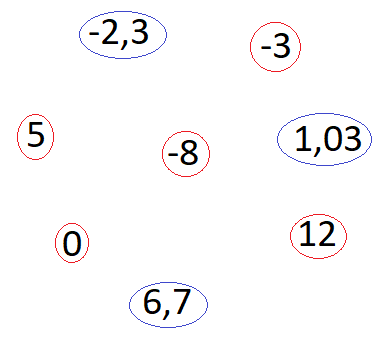
Das nächste Bild zeigt eine Reihe an Zahlen. Kreise jede Zahl rot ein, welche eine ganze Zahl ist. Alle anderen sollen blau eingekreist werden.
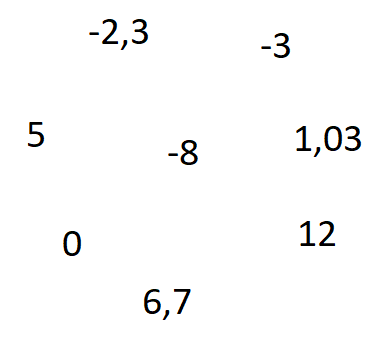
Lösung:
Alle Zahlen, die Stellen hinter dem Komma haben sind keine ganze Zahlen.
- -2,3 sowie 1,03 und 6,7
Alle Zahlen ohne Stellen hinter dem Komma sind hingegen ganzen Zahlen.
- 0, 5, -8, -3 und 12
Anzeige:
Anzeigen:
Beispiele ganze Zahlen
In diesem Abschnitt sehen wir uns eine Reihe an Beispielen zu ganzen Zahlen und deren Anwendung an. Starten wir dabei mit den Grundrechenarten, sprich wie man bei ganzen Zahlen Addition, Subtraktion, Multiplikation und Division durchführt. Weiterführende Themen werden noch im Frage- und Antwortbereich angesprochen.
Beispiel 2:
Bei der nächsten Zahlengerade soll die Addition und Subtraktion von ganzen Zahlen gezeigt werden. Berechnet werden sollen diese Aufgaben:
- -5 + 3
- +3 - 6
- -1 - 4
Lösung:
Beginnen wir mit - 5 + 3. Dies bedeutet, dass wir von der -5 um 3 nach rechts gehen. Dadurch landen wir auf der -2.
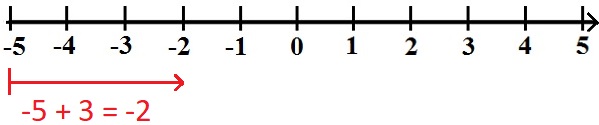
Als nächstes sehen wir uns 3 - 6 an. Dies bedeutet, dass wir von der +3 um 6 nach links gehen. Wir landen dabei auf der -3.
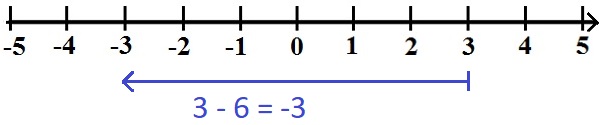
Fehlt uns noch -1 -4. Dies bedeutet, dass wir von der -1 um 4 nach links gehen. Daher landen wir auf der -5.
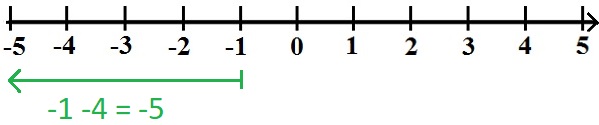
Beispiel 3:
Zeige mit einer Rechnung, wie sich negative und positive Zahlen - und zwar ganze Zahlen - mit den Vorzeichen bei der Multiplikation verhalten.
Lösung:
Ist eine der beiden Zahlen negativ, dann ist auch das Ergebnis negativ. In den anderen Fällen ist das Ergebnis positiv.
- 5 · 5 = 25
- (-5) · 5 = -25
- 5 · (-5) = -25
- (-5) · (-5) = 25
Beispiel 4:
Zeige mit einer Rechnung, wie sich negative und positive Zahlen - und zwar ganze Zahlen - mit den Vorzeichen bei der Division verhalten.
Lösung:
Ist eine der beiden Zahlen negativ, dann ist auch das Ergebnis negativ. In den anderen Fällen ist das Ergebnis positiv.
- 5 : 5 = 1
- (-5) : 5 = -1
- 5 : (-5) = -1
- (-5) : (-5) = 1
Aufgaben / Übungen ganze Zahlen
Anzeigen:Video ganze Zahlen
Ganze Zahlen Erklärung
Mit ganzen Zahlen befassen wir uns in diesem Video:
- Was ist eine ganze Zahl?
- Was ist der Unterschied zu anderen Zahlenarten?
- Beispiele und Erklärungen.
Nächstes Video »
Fragen mit Antworten ganze Zahlen
In diesem Abschnitt geht es noch um typische Fragen mit Antworten zu ganzen Zahlen.
F: Kann man auf ganze Zahlen runden?
A: Auf ganze Zahlen kann gerundet werden. So kann man zum Beispiel +2,3 auf 2 runden oder -5,9 auf -6 runden. Wie dies funktioniert lest ihr unter Runden von Zahlen (mit Regeln).
F: Gibt es eine größte oder kleinste ganze Zahl? Wie viele ganze Zahlen gibt es?
A: Es gibt keine größte oder kleinste ganze Zahl, denn man kann beliebig weiter zählen: 1, 2, 3, 4, 5, 6, usw. oder in die andere Richtung -1, -2, -3, -4, -5, -6 usw. Daher gibt es unendlich viele ganze Zahlen.
F: Wann wird dieses Thema in der Schule behandelt?
A: Das Thema ganze Zahlen wird meistens ab der 5. Klasse in der Schule behandelt. Die natürlichen Zahlen (als Teil der ganzen Zahlen) stehen schon in der 1. Klasse auf dem Plan. Da jedoch auch ein Teil der negativen Zahlen zu den ganzen Zahlen gehören, folgen diese wie gesagt erst deutlich später.
F: Welche weiteren Zahlenarten gibt es noch?
A: Weitere Zahlenarten sind:
- Natürliche Zahlen
- Negative Zahlen
- Rationale Zahlen
- Irrationale Zahlen.
- Reelle Zahlen
- Komplexe Zahlen
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
