Kreisdiagramm

Was ein Kreisdiagramm ist und wie man es selbst zeichnet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was ein Kreisdiagramm ist und welche Vorteile und Nachteile es hat.
• Beispiele um ein Kreisdiagramm selbst zu zeichnen und zu lesen.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu Kreisdiagrammen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir befassen und gleich mit dem Kreisdiagramm. Wem es nur darum geht was ein Kreisdiagramm ist, der kann gleich weiterlesen. Wer hingegen selbst eines Zeichnen möchte, der sollte Wissen was Winkel sind und wie man diese zeichnet. Noch keine Ahnung davon? Seht bitte in Mathematik Winkel und Winkel zeichnen rein.

Erklärung und Verwendung Kreisdiagramm

Was ist ein Kreisdiagramm und wofür verwendet man es? Ein Kreisdiagramm wird dazu verwendet Inhalte optisch ansprechend darzustellen. Zum Beispiel werden Kreisdiagramme gerne in den Medien genutzt um den Ausgang einer Wahl darzustellen.

Beim Kreisdiagramm handelt es sich um einen Kreis, der in verschiedene Bereiche unterteilt wird. Je größer ein Bereich ist, desto größer der Anteil. Im Fall der Wahlen hat zum Beispiel eine Partei mehr Stimmen bekommen wenn der Bereich größer ist. Damit man dies besser erkennen kann, werden die einzelnen Bereiche mit Farbe versehen.

Beispiel 1: Kreisdiagramm Erklärung

Die gültigen Stimmern einer Wahl werden in einem Kreisdiagramm dargestellt. Es nahmen vier Personen an dieser Teil. Seht zunächst einmal auf die Grafik:

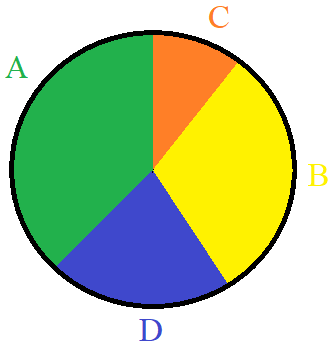
Was kann man dem Ergebnis entnehmen? Person A (grün) hat die meisten Stimmen bekommen, denn dieses Feld ist am größten. Person B (gelb) ist auf Platz 2 gelandet. Die Person D (blau) wurden Dritter. Auf dem letzten Platz ist Person C (orange) gelandet.

Bei dieser Darstellung tritt sofort ein kleines Problem auf: Hier lässt sich nicht erkennen, wie viele Stimmen oder wie viel Prozent der Stimmen die Personen bekamen. Wir sehen uns gleich an einem Beispiel zum Zeichnen von einem Kreisdiagramm an, wie man dies lösen kann. Zunächst werfen wir jedoch kurz einen Blick auf Vorteile und Nachteile von einem Kreisdiagramm.

Vorteile / Verwendung Kreisdiagramm:

• Übersichtliche Darstellung von Ergebnissen bei wenigen Teilwerten.
• Gut geeignet in vielen Medien und bei Präsentationen.
• Darstellung von Ergebnissen mit nur einer Grafik.

Nachteile / Probleme Kreisdiagramm:

• Bei zu vielen Teilwerten (Bereichen) sehr unübersichtlich.
• Zwei Kreisdiagramme zu vergleichen ist oft schwierig.
• Darstellung von negativen Werten oder Nullwerten schwierig oder unmöglich.

Anzeige:

Beispiel Kreisdiagramm zeichnen

Wir kennen nun die Vorteile, Nachteile und die Verwendung. Sehen wir und nun das Berechnen und Zeichnen von einem Kreisdiagramm mit einem Beispiel an.

Beispiel 2: Kreisdiagramm berechnen und zeichnen

Bei der Wahl zum Klassensprecher sind drei Personen angetreten. Marc bekam 15 Stimmen, Laura bekam 11 Stimmen und Florian 4 Stimmen. Zeichne das Ergebnis als Kreisdiagramm.

Lösung:

Wir haben 3 Personen, welche Stimmen bekamen. Unser Kreisdiagramm wird damit 3 Farben am Ende haben. Wir nehmen rot für Marc, blau für Laura und grün für Florian. Beim Berechnen gehen wir zunächt so vor, dass wir den Gesamtwert bestimmen. Darunter versteht man alle abgegeben Stimmen.

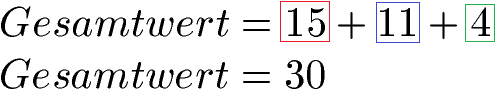
Ein Kreis hat 360 Grad und auf diese 360 Grad möchten wir die 30 Stimmen verteilen. Die Formel um die Größe (oder besser gesagt den Winkel) jeder Fläche zu berechnen lautet:

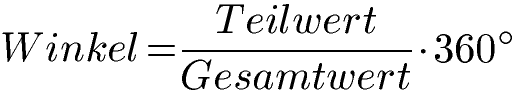
Um das Kreisdiagramm zu zeichnen, müssen wir den Winkel für Marc, Laura und Florian berechnen. Wir setzen daher die 15, die 11 und die 4 für den Teilwert ein und den Gesamtwert hatten wir zu 30 berechnet. Damit rechnen wir die drei Winkel aus:

Ein Kreis hat 360°. Wir kontrollieren daher, dass die drei Werte zusammen 360° ergeben. 180° + 132° + 48° = 360°. Dies stimmt somit. Mit diesem Wissen können wir nun das Kreisdiagramm zeichnen.

Kreisdiagramm zeichnen:

Wir brauchen zunächst einen Kreis. Zeichnet euch mit dem Zirkel, mit dem PC oder womit auch immer einen Kreis. Danach geht es darum das 1. Ergebnis einzutragen. Wir fangen mit Marc an. Ihn wollten wir in rot einzeichnen. Daher zeichnen wir in rot einen Strich. Von diesem aus fangen wir an Winkel einzutragen. Auch müsst ihr wissen wo der Kreismittelpunkt ist.

Marc hat 15 von 30 Stimmen bekommen. Wir hatten dies umgerechnet auf 180°. Und 180° entspricht einem halben Kreis. Wir machen damit den halben Kreis rot.

132 Grad entfallen auf Laura. Wir nehmen daher unser Geodreieck und legen dieses an den roten Strich an. Dies müssen wir so machen, dass die 0 vom Geodreieck im Zentrum des Kreises liegt. Bei 132 Grad auf dem Geodreieck machen wir uns eine Markierung.

Diese Markierung verbinden wir mit dem Mittelpunkt des Kreises und füllen den Bereich blau aus.

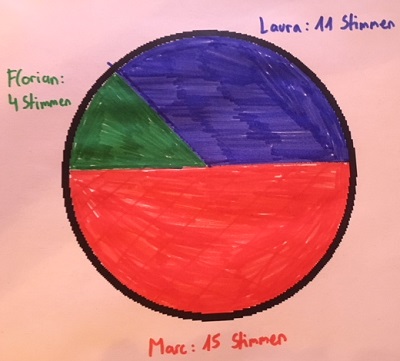
Und der Rest ist grün:

An den Rand können wir noch die Namen mit den Stimmen schreiben.

Aufgaben / Übungen Kreisdiagramm

Aufgabe 1: Wer ein Kreisdiagramm zeichnet muss dafür erst einmal einen Kreis zeichnen. In wie viel Grad wir ein Kreis eingeteilt?

• 360 Grad
• 90 Grad
• 180 Grad
• 270 Grad

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Kreisdiagramm

Fragen mit Antworten zum Kreisdiagramm