Lineare Abhängigkeit von 2 Vektoren (Unabhängigkeit)

Die lineare Abhängigkeit bzw. lineare Unabhängigkeit von 2 Vektoren sehen wir uns hier an. Dies sind die Themen:

• Eine Erklärung, was lineare Abhängigkeit (Unabhängigkeit) bedeutet.
• Beispiele um 2 Vektoren auf lineare Abhängigkeit zu prüfen.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur linearen Abhängigkeit bzw. Unabhängigkeit.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Um die lineare Abhängigkeit von 2 Vektoren zu verstehen, ist es hilfreich, wenn ihr bereits wisst, was ein Vektor ist. Wer davon noch keine Ahnung hat wirft erst einmal einen Blick in die Vektoren Grundlagen.

Lineare Abhängigkeit von 2 Vektoren

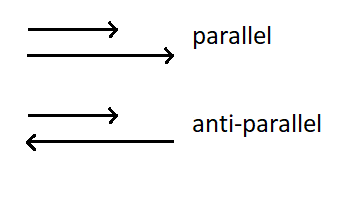
Verlaufen 2 Vektoren parallel oder anti-parallel, nennt man diese kollinear. Die Vektoren sind Vielfache voneinander. In diesem Fall sind die Vektoren linear abhängig.

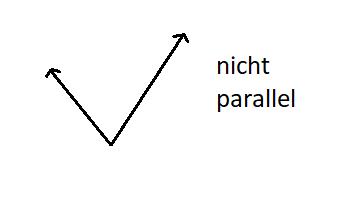
Nicht parallele Vektoren

Das Gegenteil sind zwei Vektoren, die nicht parallel sind. Diese sind somit nicht kollinear, die beiden Vektoren sind keine Vielfache voneinander. Die beiden Vektoren sind nicht linear abhängig (= linear unabhängig).

Im nächsten Abschnitt sehen wir uns Beispiele zur linearen Abhängigkeit von 2 Vektoren an.

Anzeige:

Beispiele lineare Abhängigkeit (Unabhängigkeit) 2 Vektoren

Im ersten Beispiel weisen wir die lineare Abhängigkeit von 2 Vektoren nach. Im zweiten Beispiel weisen wir die lineare Unabhängigkeit von 2 Vektoren nach.

Beispiel 1: Lineare Abhängigkeit 2 Vektoren

Wir haben zwei Vektoren gegeben. Sind die 2 Vektoren linear abhängig?

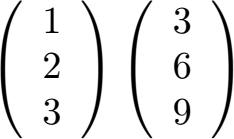
Lösung:

Um dies zu prüfen, müssen wir herausfinden, ob die beiden Vektoren Vielfache voneinander sind. Wir bilden daher 3 Gleichungen und berechnen jeweils k.

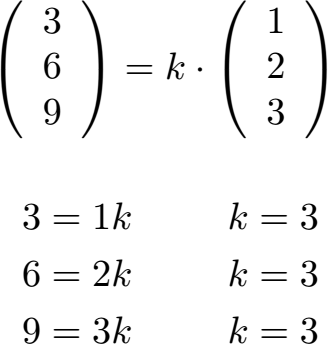
Mit k = 3 können wir jede der drei Gleichungen lösen. Die beiden Vektoren sind Vielfache voneinander. Daher sind die beiden Vektoren linear abhängig.

Beispiel 2: Lineare Unabhängigkeit 2 Vektoren

Wir haben zwei Vektoren gegeben. Sind die 2 Vektoren linear abhängig?

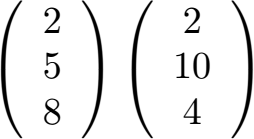
Lösung:
Auch in diesem Fall stellen wir drei Gleichungen auf. Zeile für Zeile. Damit berechnen wir jeweils k.

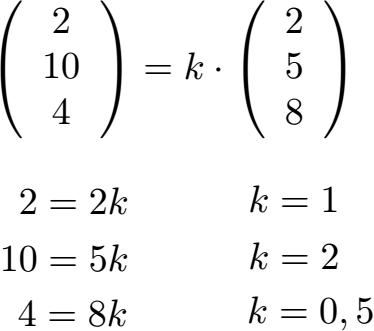
Wir sehen, dass k verschieden ist. Die beiden Vektoren sind keine Vielfachen voneinander und daher linear nicht abhängig. Sie sind also linear unabhängig.

Aufgaben / Übungen lineare Abhängigkeit

Aufgabe 1:

In diesem Bereich erhaltet ihr die Möglichkeit das Spatprodukt zu üben. Da einige Schüler und Studenten jedoch bereits an einfachen Fragen scheitern, gibt es bei uns auch Fragen zum Thema.

• Ergänze den Satz: Verlaufen Vektoren parallel oder anti-parallel nennt man diese kollinear. Die Vektoren sind Vielfache voneinander, also....

• rechtwinklig zueinander
• stumpfwinklig zueinander
• linear abhängig
• linear unabhängig

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video lineare Abhängigkeit

Fragen mit Antworten zur linearen Abhängigkeit bei 2 Vektoren