Was ist ein Vektor? Vektoren Grundlagen

Was ist ein Vektor? Dies sehen wir uns hier an. Die Themen:

• Eine Erklärung, was ein Vektor ist und wozu man diesen braucht.
• Beispiele für die Verwendung von Vektoren.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu den Grundlagen der Vektorrechnung.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Ihr solltet bereits Koordinatensysteme kennen. Diese gibt es in der Ebene mit dem x-y-Koordinatensystem und im Raum mit dem x-y-z Koordinatensystem. Ihr solltet dabei auch wissen wie man Punkte in ein Koordinatensystem einträgt.

Vektor Definition und Vektor ablesen

Was ist überhaupt ein Vektor? Um dies zu verstehen - und auch wozu man einen Vektor braucht - nehmen wir uns einmal ein Koordinatensystem. In dieses zeichnen wir zwei Punkte ein mit A(1|0) und B(4|2).

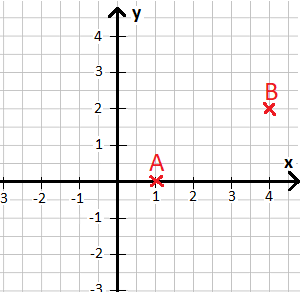
Wie kommt man in der Mathematik von A nach B? Dies muss man irgendwie doch angeben können? Dies geht auch und führt uns zum Begriff des Vektors. Grafisch handelt es sich dabei um einen Pfeil wie im nächsten Koordinatensystem eingezeichnet.

Vektor einzeichnen oder ablesen:

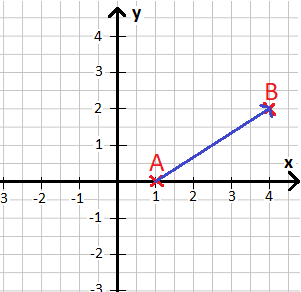
Man kann einen Vektor ablesen. Der Vektor sagt in diesem Fall aus, dass ich von A nach B komme, indem ich um 3 nach rechts und 2 nach oben gehe. Ein Vektor erkennt man an einem Pfeil über einem Buchstaben oder an einem Pfeil über zwei Buchstaben (wie den beiden Punkten in der letzten Grafik):

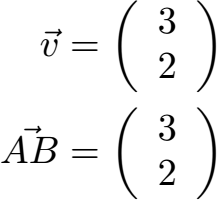
Sehen wir uns noch eine Definition für einen Vektor an:

Anzeige:

Vektoren Beispiel und Begriffe

Sehen wir uns einmal ein Beispiel für die Verwendung von einem Vektor an. Nehmen wir dazu einen Klotz, der bewegt werden soll. Um dies zu erreichen ziehen wir an dem Klotz. Die Kraft die dabei eingesetzt wird bezeichnet man oft mit einem F. Über diesem F ist ein Pfeil, denn die Kraft wirkt in eine bestimmte Richtung.

Bei einer physikalischen oder technischen Vektorgröße sollte man die Maßeinheit noch mit angeben. Im Falle einer Kraft wäre dies eine Angabe in Newton, zum Beispiel 100 N.

Vektoren Begriffe

Rund um Vektoren tauchen immer wieder einige wichtige Begriffe und Eigenschaften auf. Diese solltet ihr kennen:

• Vektoren haben eine Länge (auch Betrag genannt).
• Vektoren haben eine bestimmte Richtung.
• Stimmen Länge und Richtung zweier Vektoren überein nennt man diese gleich.
• Zwei Vektoren mit gleicher Richtung nennt man parallel.
• Haben zwei Vektoren eine entgegengesetzte Richtung sind sie anti-parallel.
• Startet ein Vektor im Ursprung des Koordinatensystems (x = 0, y = 0 und im Raum noch z = 0) nennt man diesen Ortsvektor.
• Startet ein Vektor nicht im Ursprung des Koordinatensystems nennt man diesen Richtungsvektor.

Aufgaben / Übungen Vektor Grundlagen

Aufgabe 1: In diesem Bereich könnt ihr die Grundlagen der Vektorrechnung üben. Leider ist es oft so, dass viele Schüler und auch Studenten bereits an Begriffen zur Vektorrechnung scheitern. Daher bieten wir hier neben Aufgaben mit Zahlen auch noch ein paar Fragen zum Thema an.

• Welche Aussage zur nächsten Grafik ist richtig?

• Die Kraft ist Null.
• Der Klotz bewegt sich mit 3 Meter pro Sekunde.
• Eine Kraft wirkt in eine bestimmte Richtung.
• Alle Kräfte neutralisieren sich.

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Grundlagen Vektoren

Fragen mit Antworten zu den Grundlagen der Vektorrechnung