Lineare Abhängigkeit von 3 Vektoren (Unabhängigkeit)

Die lineare Abhängigkeit bzw. lineare Unabhängigkeit von 3 Vektoren sehen wir uns hier an. Dies sind die Themen:

• Eine Erklärung, was lineare Abhängigkeit (Unabhängigkeit) bedeutet.
• Beispiele um 3 Vektoren auf lineare Abhängigkeit oder Unabhängigkeit zu prüfen.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur linearen Abhängigkeit bzw. Unabhängigkeit.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Die lineare Abhängigkeit von 3 Vektoren kann man entweder über das Lösen eines linearen Gleichungssystems prüfen oder über Determinanten. Wir sehen uns beide Verfahren hier noch an. Wer die Berechnung dennoch nicht nachvollziehen kann sollte das dabei verlinkte Vorwissen sich doch noch einmal genauer ansehen.

Lineare Abhängigkeit: Erklärung und LGS

Klären wir zunächst was man unter linearer Abhängigkeit oder linearer Unabhängigkeit von 3 Vektoren versteht. Dazu sehen wir uns zwei Grafiken an. In der ersten Grafik haben wir 3 Vektoren, die sich in einer Ebene befinden. Man nennt dies komplanar und dieses Vektoren sind linear abhängig.

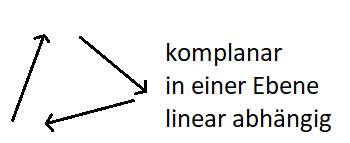
In der zweiten Grafik ist dies nicht so. Der linke Vektor zeigt nach oben während die anderen beiden Vektoren nach rechts unten oder links unten zeigen. Diese Vektoren liegen nicht in einer Ebene. Man bezeichnet dies als nicht komplanar und die Vektoren sind linear unabhängig.

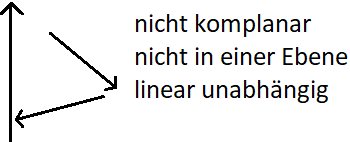
Wie kann man 3 Vektoren rechnerisch auf lineare Abhängigkeit prüfen? Dazu gibt es 2 Möglichkeiten:

• Lineares Gleichungssystem aufstellen und lösen
• Determinante aufstellen und berechnen

Beide Lösungswege sehen wir uns hier einmal an.

Beispiel 1: LGS lösen

Wir haben drei Vektoren. Prüfe mit einem linearen Gleichungssystem (kurz LGS), ob diese drei Vektoren linear Abhängig sind oder nicht.

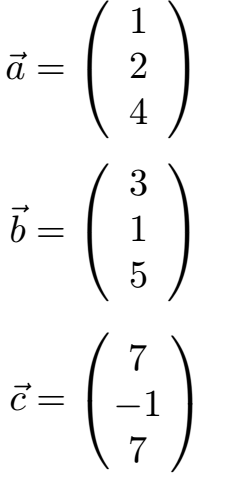
Lösung:

Mit den drei Vektoren stellen wir ein lineares Gleichungssystem auf. Wer nicht weiß was dies ist wirft einen Blick in lineare Gleichungssysteme lösen. Dieses Gleichungssystem besteht aus drei Zeilen mit drei Unbekannten (r, s und t). Auf der rechten Seite der Gleichung haben wir eine Null.

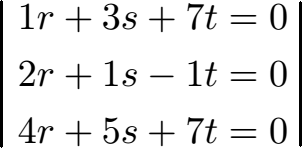
Dieses lineare Gleichungssystem müssen wir lösen. Dazu gibt es verschiedene Möglichkeiten. In der Oberstufe wird oft von den Schülern verlangt den Gauß Algorithmus zum Lösen zu verwenden. Daher verwenden wir diesen auch hier. Wer den folgenden Rechenweg nicht versteht, kann gerne noch einmal in den Hauptartikel Gauß Algorithmus reinsehen.

Um die Schreibarbeit zu verringern lassen wir das r, s und t einmal weg. Da dies dann auch keine Gleichungen mehr sind kommen die Nullen hinter einen Strich.

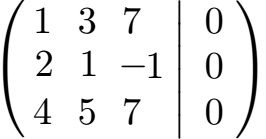
Das Ziel vom Gauß-Verfahren besteht darin Nullen zu erzeugen. In der mittleren Zeile soll vorne eine Null stehen. In der unteren Zeile sollen die ersten beiden Spalten jeweils eine 0 sein. Um dies zu erreichen, versuchen wir in der ersten Spalte jeweils die gleiche Zahl zu erzeugen. In unserem Fall wäre es am einfachsten eine 4 zu erzeugen. Dazu müssen wir alle Zahlen der ersten Zeile mit 4 multiplizieren und alle Zahlen der zweiten Zahl mit 2 multiplizieren.

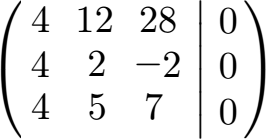
Jetzt nehmen wir die erste Zeile und subtrahieren die zweite Zeile: 4 - 4 = 0, 12 - 2 = 10 und 28 - (-2) = 30. Danach nehmen wir die erste Zeile und subtrahieren die dritte Zeile: 4 - 4 = 0, 12 - 5 = 7 und 28 - 7 = 21.

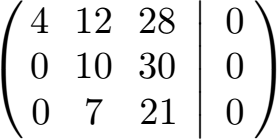
In Zeile 2 und 3 haben wir vorne bereits eine Null. Als nächstes brauchen wir in der mittleren Spalte zwei gleiche Zahlen in der mittleren und unteren Zeile. Dazu multiplizieren wir die mittlere Zeile mit 7 und die untere Zeile mit 10.

Die mittlere Zeile minus der unteren Zeile ergibt 70 - 70 = 0 und 210 - 210 = 0. Der Rest sind ebenfalls Nullen.

Wir haben eine Nullzeile unten. Eine Nullzeile bedeutet, dass die 3 Vektoren linear Abhängig sind.

Anzeige:

Lineare Abhängigkeit: Determinante und Variable

Neben dem Lösen eines linearen Gleichungssystems gibt es noch eine weitere Möglichkeit die lineare Abhängigkeit oder Unabhängigkeit von 3 Vektoren zu prüfen. Dazu verwenden wir eine Determinante. Außerdem zeigen wir euch noch was nötig ist um eine Variable so zu berechnen, dass 3 Vektoren linear Abhängig werden.

Beispiel 2: Determinante verwenden

Zeige mit einer Determinante, ob diese drei Vektoren linear abhängig oder linear unabhängig sind.

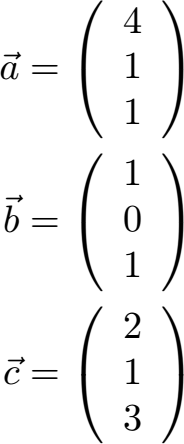
Lösung:

Die drei Vektoren schreiben wir in eine Determinante. Die 9 Zahlen stehen damit zwischen zwei Strichen.

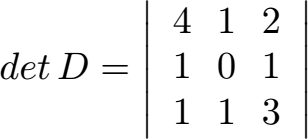
Wie berechnet man die Determinante? Die allgemeine Beschreibung dazu ist diese:

Jetzt müssen wir einfach nur die Zahlen einsetzen.

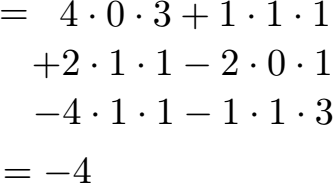
Wir erhalten als Ergebnis der Determinante -4. Die Vektoren sind daher linear unabhängig, sie liegen daher nicht in einer Ebene.

Beispiel 3: Vektoren mit Variable linear abhängig machen

Was müsste beim letzten Beispiel verändert werden damit die Vektoren linear abhängig werden?

Lösung: Der erste Vektor beinhaltete die Zahlen 4, 1 und 1. Macht man daraus 4, 1 und 5 und berechnet danach die Determinante, dann wird diese 0. Wer es nicht glaubt, rechnet noch einmal nach. Ihr könnt anstatt der 4, 1 und 1 oder 4, 1 und 5 einfach 4, 1 und z einsetzen. Rechnet ihr die Determinante aus erhaltet ihr z - 5 = 0. Daher ist z = 5 wenn die Vektoren linear abhängig werden sollen.

Aufgaben / Übungen lineare Abhängigkeit und Unabhängigkeit

Aufgabe 1:

In diesem Bereich erhaltet ihr die Möglichkeit das Spatprodukt zu üben. Da einige Schüler und Studenten jedoch bereits an einfachen Fragen scheitern, gibt es bei uns auch Fragen zum Thema.

• Ergänze den Satz: Verlaufen Vektoren parallel oder anti-parallel nennt man diese kollinear. Die Vektoren sind Vielfache voneinander, also....

• rechtwinklig zueinander
• linear unabhängig
• linear abhängig
• stumpfwinklig zueinander

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video lineare Abhängigkeit (Unabhängigkeit)

Fragen mit Antworten lineare Abhängigkeit 3 Vektoren