Lineare Gleichungssysteme lösen
Geschrieben von: Dennis RudolphFreitag, 13. Dezember 2019 um 18:28 Uhr
Wir sehen uns an hier an, wie man lineare Gleichungssysteme löst. Die Themen:
- Eine Erklärung, was lineare Gleichungssysteme sind und wie man sie löst.
- Beispiele zum Lösen durch Einsetzungsverfahren, Gleichsetzungsverfahren, Additionsverfahren, Gauß etc.
- Aufgaben / Übungen zu linearen Gleichungssystemen.
- Mehrere Videos zu Gleichungssystemen.
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Tipp: Ihr solltet bereits einfache Gleichungen lösen können. Wer dies noch nicht kann wirft bitte erst einmal einen Blick in Gleichungen auflösen.
Erklärung lineare Gleichungssysteme
Starten wir kurz mit einer Definition, was ein (lineares) Gleichungssystem überhaupt ist:
Unter einem Gleichungssystem versteht man zwei oder mehr Gleichungen, welche gemeinsam gelöst werden müssen. Ziel bei der Berechnung ist es, für jede Variable eine Zahl zu finden, die alle Gleichungen korrekt löst. Das Gleichungssystem wird als linear bezeichnet, wenn nur lineare Gleichungen vorkommen.
Es gibt zahlreiche verschiedene Möglichkeiten ein solches Gleichungssystem zu lösen. Wenn ihr bereits wisst, welches Verfahren ihr verwendet möchtet, dann könnt ihr gleich aus der folgenden Liste das entsprechende Verfahren aussuchen. Ansonsten lest unterhalb weiter, denn dort werden diese vorgestellt.
Verfahren für lineare Gleichungssysteme:
- Gleichsetzungsverfahren
- Einsetzungsverfahren
- Additionsverfahren / Subtraktionsverfahren
- Gauß-Verfahren / Gauß-Verteilung
- Gleichungssysteme Sonderfälle
Gleichsetzungsverfahren:
Beim Gleichsetzungsverfahren ist jede Gleichung nach der selben Variablen (Unbekannten) aufzulösen und diese beiden Gleichungen sind danach gleichzusetzen. Damit wird die zweite Unbekannte berechnet und rückwärts eingesetzt. Klingt schwierig, ist aber ganz einfach.
Beispiel: Gelöst werden soll das folgende lineare Gleichungssystem mit dem Gleichsetzungsverfahren bei 2 Variablen. Wie groß sind x und y?
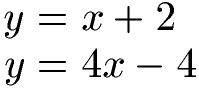
Lösung:
Hier sind beide Gleichungen bereits nach y aufgelöst. Die beiden Gleichungen sagen aus, dass y so groß ist wie x + 2 und das y auch so groß ist wie 4x - 4. Dies bedeutet, dass x + 2 und 4x - 4 gleich groß sind. Wir nutzen dies aus, indem wir sie gleichsetzen.
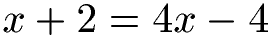
Wir haben damit eine Gleichung mit nur einer Unbekannten (x). Diese lineare Gleichung lösen wir nach x auf.
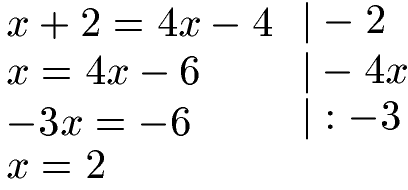
Wir haben damit x = 2 berechnet. Dies setzen wir in eine der beiden Startgleichungen ein und berechnen damit y.
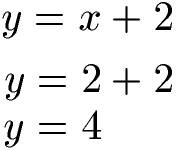
Um dies zu kontrollieren setzen wir x = 2 und y = 4 noch einmal in die andere Gleichung ein. Dabei stehen wir, dass auch diese Gleichung korrekt gelöst wird.
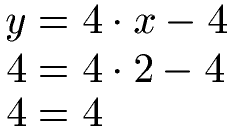
Wir können mit x = 2 und y = 4 noch eine Lösungsmenge angeben:
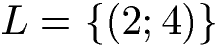
Wie man lineare Gleichungssysteme mit dem Gleichsetzungsverfahren löst lernt ihr im Artikel Gleichsetungsverfahren (lineare Gleichungssysteme).
Anzeige:
Anzeigen:
Gleichungssysteme Einsetzungsverfahren, Additionsverfahren und Gauß
In diesem Abschnitt sehen wir uns weitere Verfahren zum Lösen von Gleichungssystemen an. Dabei sehen wir uns zunächst das Einsetzungsverfahren an. Danach gibt es das Additionsverfahren bzw. Subtraktionsverfahren. Als Letztes sehen wir uns das Gauß-Verfahren bzw. den Gauß-Algorithmus an.
Einsetzungsverfahren:
Beim Einsetzungsverfahren geht es darum, dass man eine der Gleichungen nach einer Unbekannten auflöst und diesen Ausdruck in die nächste Gleichung des Systems einsetzt. Das Einsetzungsverfahren eignet sich oft bei Gleichungssystemen mit 2 oder 3 Gleichungen bzw. 2 oder 3 Unbekannten.
Beispiel: Wir haben zwei Gleichungen mit 2 Variablen (x,y). Löse das Gleichungssystem mit dem Einsetzungsverfahren.
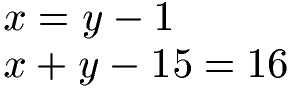
Lösung:
Die oberste Gleichung ist bereits nach x aufgelöst. Dies nutzen wir aus, denn wir wissen, dass x so groß ist wie y - 1. Dieses y - 1 setzen wir für die Variable x in die zweite Gleichung ein. Danach lösen wir nach y auf und erhalten y = 16.
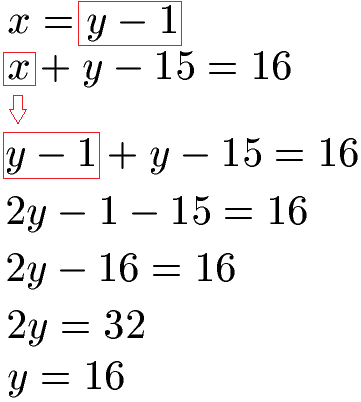
Mit y = 16 gehen wir noch in die erste lineare Gleichung rein und berechnen noch x = 15.
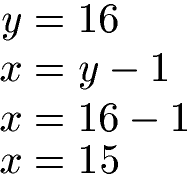
Mit x = 15 und y = 16 können wir beide Gleichungen korrekt lösen. Wir haben damit das Ergebnis des linearen Gleichungssystems gefunden.
Weitere Erklärungen und Beispiele findet ihr unter Einsetzungsverfahren.
Additionsverfahren / Subtraktionsverfahren:
Eine weitere Möglichkeit ein lineares Gleichungssystem zu lösen ist das Additionsverfahren bzw. Subtraktionsverfahren. Beim Additionsverfahren (Subtraktionsverfahren) versucht man zwei oder drei Gleichungen so umzuformen, dass man durch Addition oder Subtraktion eine Unbekannte verschwinden lassen kann.
Beispiel: Wir haben ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten (x und y). Löse dieses mit dem Additionsverfahren. Wie groß sind x und y?
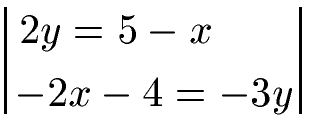
Lösung:
Zunächst sortieren wir beide Gleichungen etwas um. Wir bringen alle Terme mit Variablen auf die linke Seite der Gleichung und die reinen Zahlen auf die rechte Seite der Gleichung. Dies machen wir auch so, dass die Terme mit x und y jeweils untereinander stehen.
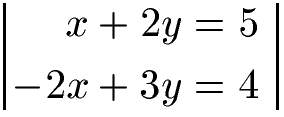
Wir multiplizieren die erste Gleichung mit 2.
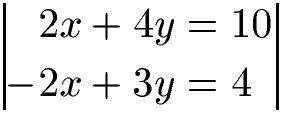
Wir haben jetzt zwei passendere Gleichungen. In der ersten Gleichung haben wir 2x vorne und darunter -2x. Würden wir jetzt diese Gleichungen addieren fliegt die Variable x raus. Wir haben 2x + (- 2x) = 0 vorne. Außerdem 4y + 3y = 7y und 10 + 4 = 14. Wir erhalten 7y = 14 und damit y = 2.
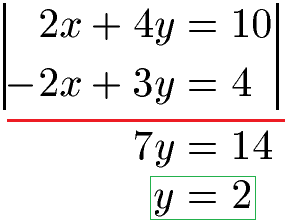
Wir wissen nun, dass y = 2 ist. Damit wollen wir noch x berechnen. Daher nehmen wir von weiter oben eine Gleichung und setzen y hier ein.
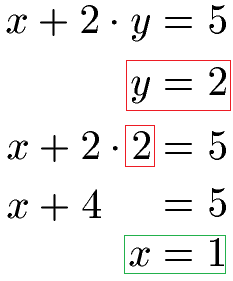
Wir berechnen damit x = 1 und y = 2 als Lösung beider Gleichungen des Gleichungssystems.
Weitere Beispiele und Erklärungen zu diesem Lösungsverfahren für lineare Gleichungssysteme findet ihr unter Additionsverfahren / Subtraktionsverfahren.
Gauß-Verfahren / Gauß Eliminationsverfahren:
Neben den bislang vorgestellten Möglichkeiten ein lineares Gleichungssystem zu lösen gibt es noch den Gauß-Algorithmus. Hier geht man so vor, dass ein Gleichungssystem entsteht, bei dem in der ersten Zeile alle Variablen enthalten sind und in jeder weiteren Zeile darunter je eine Variable beseitigt wurde.
Beispiel: Wir haben ein Gleichungssystem mit drei Gleichungen und drei Variablen. Dieses soll mit dem Gauß-Algorithmus gelöst werden. Wie groß sind x, y und z?
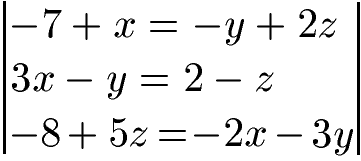
Lösung:
Zunächst bringen wir alle Unbekannten (x, y und z) auf die linke Seite der Gleichung und nur die Zahlen auf die rechte Seite der Gleichung. Dabei sollen alle Angaben mit x, y und z jeweils untereinander stehen.
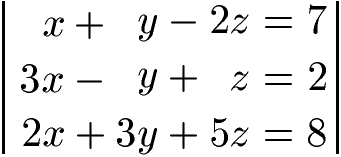
Zunächst wollen wir x beseitigen. Durch Multiplikation bzw. Division bei allen Gleichungen sollen gleiche Faktoren erzeugt werden. Dies erreichen wir hier, indem wir 6x bei jeder Gleichung erzeugen. Daher multiplizieren wir die erste Gleichung mit 6, die zweite Gleichung mit 2 und die dritte Gleichung multiplizieren wir mit 3. Dadurch erhalten wir:
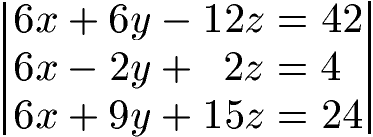
Jetzt können wir subtrahieren:
- Wir nehmen die 1. Gleichung und subtrahieren davon die 2. Gleichung. Vorne erhalten wir 6x - 6x = 0. Danach 6y - (-2y) = 8y und -12z - 2z = -14z. Auf der rechten Seite der Gleichung 42 - 4 = 38.
- Wir nehmen die 2. Gleichung und subtrahieren davon die 3. Gleichung. Vorne erhalten wir 6x - 6x = 0. Danach 6y - 9y = -3y. Außerdem -12z -15z = -27z. Auf der rechten Seite der Gleichung 42 - 24 = 18.
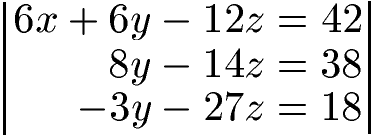
Mit 8y -14z = 38 und -3y - 27z = 18 haben wir nun nur noch noch zwei Gleichungen mit zwei Variablen. Als nächstes werfen wir y raus. Um dies zu erreichen multiplizieren wir die 2. Gleichung mit 3 und die 3. Gleichung mit 8.
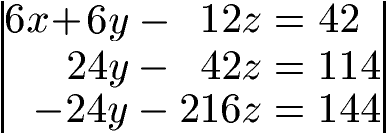
Jetzt können wir addieren: Die 2. Gleichung plus die 3. Gleichung. Wir erhalten 24y + (-24y) = 0. Außerdem -42z + (-216z) = -258z. Auf der rechten Seite erhalten wir 114 + 144 = 258.
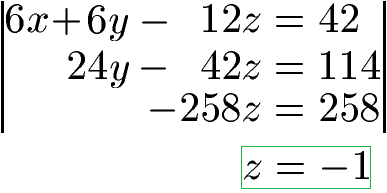
Durch -258z = 258 erhalten wir z = -1 als ersten Teil der Lösung. Dies setzen wir in die 2. Gleichung 24y -42z = 114 ein und berechnen damit y = 3.
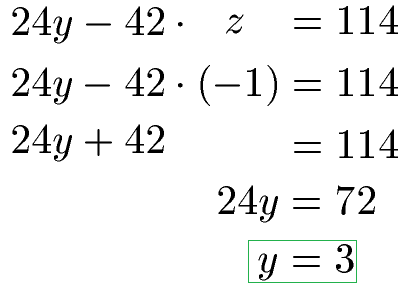
Mit y und z gehen wir in eine Gleichung mit allen Unbekannten und rechnen noch x aus.
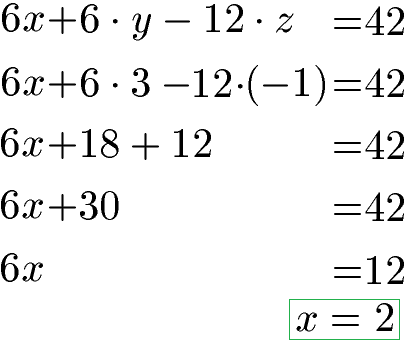
Mehr zu diesem Lösungsverfahren findet ihr unter Gauß-Verfahren / Gauß-Algorithmus.
Aufgaben / Übungen lineare Gleichungssysteme
Anzeigen:Video lineare Gleichungssysteme
Erklärung und Beispiele
In diesem Video wird erklärt, was ein Gleichungssystem ist. Ein Gleichungssystem wird dort als Gleichungen mit mehreren Variablen erklärt, für die eine gemeinsame Lösung gefunden werden soll. Anhand von drei Verfahren erklärt das Lernvideo anschaulich, wie Gleichungssysteme gelöst werden können. Mithilfe des Einsetzungsverfahrens, des Gleichsetzungsverfahrens sowie des Additionsverfahrens werden in dem Videobeitrag Gleichungen gelöst. Für alle Lösungsansätze werden die gleichen Beispiele verwendet. Diese sind:
x + y = 2 und x - y = -8
Im ersten Abschnitt wird das Einsetzungsverfahren erklärt. Mithilfe dieser Lösungsvariante werden die Gleichungen nach einer Variablen umgestellt und so gelöst. Zunächst wird also eine der beiden Gleichungen nach einer Variablen umgestellt und die daraus entstandene Gleichung in die zweite Gleichung eingesetzt. Daher kommt auch der Name "Einsetzungsverfahren".
Im zweiten Teil des Lernvideos geht es im Gleichsetzungsverfahren um Gleichungen, die nach einer Variablen umgestellt werden und deren Terme dann gleichgesetzt werden.
Der dritte und letzte Abschnitt des Videos behandelt das Additionsverfahren. In Gleichungen mit Variablen mit gleichen Koeffizienten aber umgekehrten Vorzeichen wird durch das Additionsverfahren eine Lösung gefunden.
Besonders wichtig zu wissen ist, dass alle Verfahren bei identischen Gleichungen zur gleichen Lösung führen. Quelle: Youtube.com.
Nächstes Video »
Fragen mit Antworten lineare Gleichungssysteme lösen
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zu linearen Gleichungssystemen und deren Lösung an.
F: Wann setze ich welches Verfahren zum Lösen von Gleichungssystemen ein?
A: Das Gleichsetzungsverfahren und das Einsetzungsverfahren sind oft praktisch wenn das Gleichungssystem aus nur 2 Gleichungen besteht. Man kann mit diesen Verfahren natürlich auch größere Systeme lösen, dies wird jedoch meistens sehr unschön bei der Rechnung. Bei 3 Gleichungen funktioniert das Additionsverfahren / Subtraktionsverfahren in der Regel relativ gut. Alternativ kann man bei 3 Gleichungen oder mehr das Gauß-Verfahren / Gauß-Verteilung verwenden. Dieses kann man auch in Matrix-Schreibweise einsetzen.
F: Welche "Sonderfälle" gibt es bei Gleichungssystemen?
A: Startet man in der Schule mit dem Lösen von Gleichungen und Systemen, dann gibt es dafür eigentlich immer eine richtige Lösung. Gemeint ist damit, dass man für x, y oder andere Variablen Zahlen berechnet, welche alle Gleichungen korrekt löst. Doch später kommen Spezialfälle dazu. So lassen sich manche Gleichungssysteme gar nicht lösen oder es gibt unendlich viele Lösungen. Außerdem können diese unterbestimmt bzw. überbestimmt sein. Solche Fälle sehen wir uns an unter Gleichungssysteme unterbestimmt, überbestimmt, unlösbar und unendlich viele Lösungen.
F: Wie vermeide ich Fehler beim Rechnen?
Wer sich immer wieder verrechnet sollte über dies nachdenken:
- Nach jedem Rechenschritt diese Rechnung noch einmal (zumindest im Kopf) durchführen.
- Den durchgeführten Schritt rückwärts noch einmal rechnen.
- Am Ende der Berechnung die Zahlen für die Variablen in die Ausgangsgleichungen einsetzen.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
