Magische Quadrate lösen 3x3 / 4x4

Mit magischen Quadraten - oft auch Zauberquadrate genannt - befassen wir uns in diesem Artikel. Dies sehen wir uns dazu an:

• Eine Erklärung, was magische Quadrate sind und wie man sie löst.
• Viele Beispiele zum Umgang mit magischen Quadraten.
• Aufgaben / Übungen damit ihr selbst das Thema üben könnt.
• Ein Video zu magischen Quadraten.
• Ein Frage- und Antwortbereich rund um Zauberquadrate / magische Quadrate.

Zunächst soll kurz erwähnt werden, dass manche Menschen die magischen Quadrate auch als Zauberquadrate bezeichnen. Wir haben dies so unterteilt, dass wir die Einführung unter Zauberquadrate machen und die Fortsetzung hier zeigen, auch mit größeren magischen Quadraten.

Erklärung: Magische Quadrate 3x3 und 4x4

Starten wir mit einer Erklärung zu magischen Quadraten. Dabei nehmen wir ein magisches Quadrat mit 3x3, also 9 Felder. Über diesen 9 Feldern steht eine Summe, die manchmal auch Zaubersumme genannt wird. Schaut einmal auf die nächste Grafik, die wir im Anschluss besprechen.

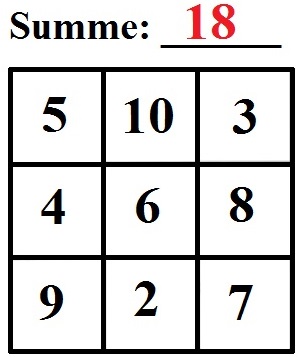
Wie funktioniert ein magisches Quadrat nun? Bei magischen Quadraten sind die Summen in den Zeilen, Spalten und Diagonalen gleich groß. Schauen wir uns dies für das Zauberquadrat von eben einmal an.

• Zeile oben: 5 +10 + 3 = 18
• Zeile mitte: 4 + 6 + 8 = 18
• Zeile unten: 9 + 2 + 7 = 18

• Spalte links: 5 + 4 + 9 = 18
• Spalte mitte: 10 + 6 + 2 = 18
• Spalte rechts: 3 + 8 + 7 = 18

• schräg: 5 + 6 + 7 = 18
• schräg: 9 + 6 + 3 = 18

Wie man sehen kann: In allen Fällen erhalten wir eine Summe von 18. Wie man selbst solche magischen Quadrate lösen kann, seht ihr unten in Beispielen. Zuvor jedoch noch ein magisches Quadrat mit 4x4.

Magisches Quadrat 4x4:

Nehmen wir noch ein größeres magisches Quadrat mit 4x4. Wir haben damit 16 Felder. Auch hier gilt, dass alle Zeilen, Spalten und Diagonalen jeweils eine identische Summe ergeben müssen. Werft einmal einen Blick auf das nächste magische Quadrat, im Anschluss folgt die Erklärung:

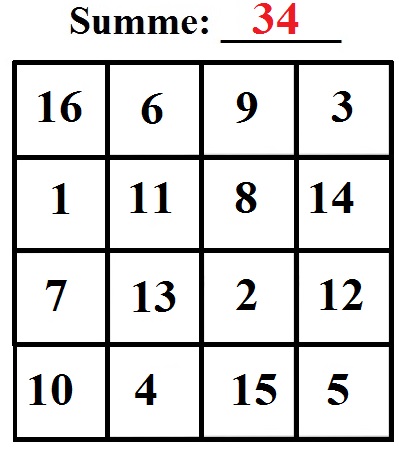
Die Summe lautet 34. Die Rechnung sieht so aus:

• 1. Zeile: 16 + 6 + 9 + 3 = 34
• 2. Zeile: 1 + 11 + 8 + 14 = 34
• 3. Zeile: 7 + 13 + 2 + 12 = 34
• 4. Zeile: 10 + 4 + 15 + 5 = 34
• 1. Spalte: 16 + 1 + 7 + 10 = 34
• 2. Spalte: 6 + 11 + 13 + 4 = 34
• 3. Spalte: 9 + 8 + 2 + 15 = 34
• 4. Spalte: 3 + 14 + 12 + 5 = 34
• 1. Diagonale: 16 + 11 + 2 + 5 = 34
• 2. Diagonale: 3 + 8 + 13 + 10 = 34

Anzeige:

Beispiele magische Quadrate 3x3 und 4x4

Wir hatten oben zwei ausgefüllte magische Quadrate. In der Schule (Grundschule) müssen Schüler und Schülerinnen diese selbst ausfüllen. Daher nehmen wir einfach die beiden magischen Quadrate von oben und stellen diese als Aufgabe, wie eben in der Schule.

Beispiel 1: 3x3

Fülle das magische Quadrat 3x3 aus.

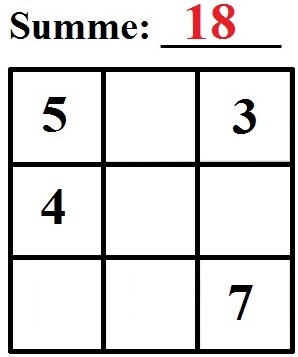
Wir wissen, dass die Summe 18 sein muss. Damit können wir zum Beispiel oben und rechts die beiden Zahlen ergänzen:

• 5 + 3 + ___ = 18, die 10 fehlt.
• 3 + 7 + ___ = 18, die 8 fehlt.

Die führt uns zu:

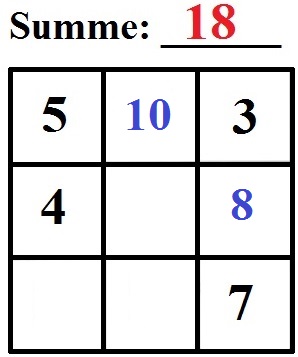
Die Felder links unten und in der Mitte können wir ausfüllen:

• 5 + 4 + ___ = 18, also 9 eintragen.
• 5 + 7 + ___ = 18, also 6 eintragen.

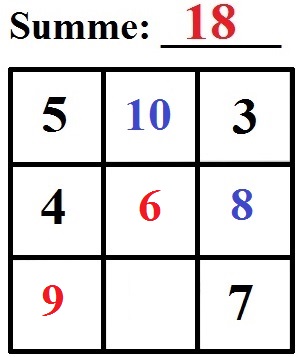
Fehlt noch die Zahl unten:

• 9 + 7 + ____ = 18, die 2 fehlt.

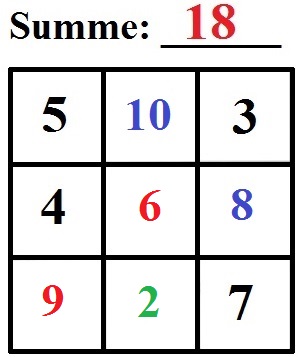
Beispiel 2:

Auch das zweite Beispiel dürfte euch bekannt vorkommen. Dabei entfernen wir die Zahlen vom 4x4 Beispiel von oben und füllen die Aufgabe aus. Der Start sieht so aus:

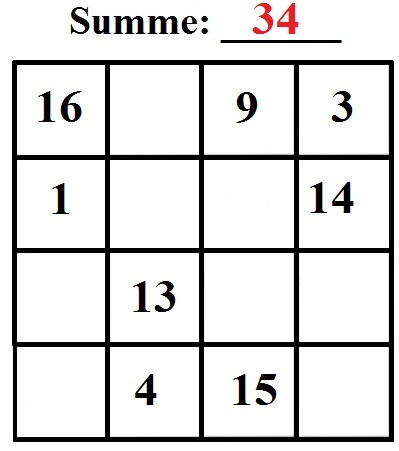
Gehen wir es an: Die Zahl oben können wir ergänzen und im Anschluss die Zahl darunter:

• 16 + ___ + 9 + 3 = 34 und wir ergänzen die 6.
• 6 + ___ + 13 + 4 = 34 und wir ergänzen die 11.

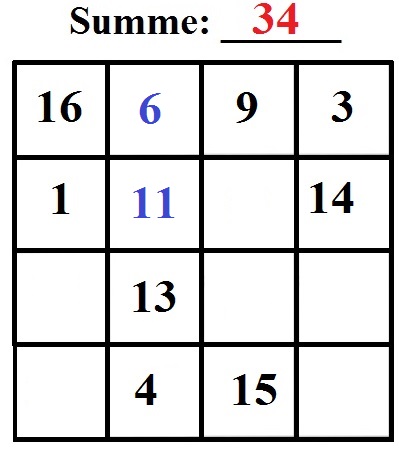
Damit können wir das Feld rechts von der 11 berechnen und auch das Feld ganz links unten über die Diagonale.

• 1 + 11 + ___ + 14 = 34 und wir ergänzen die 8.
• 3 + 8 + 13 + ___ = 34 und wir ergänzen die 10.

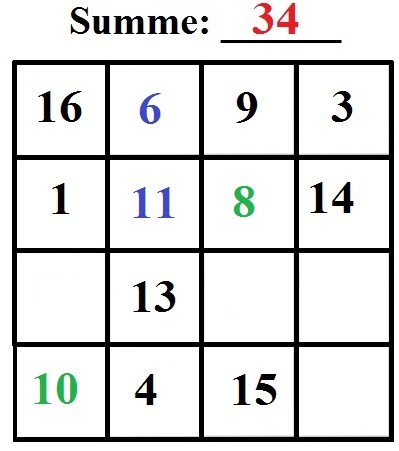
In der 3. Zeile können wir zwei weitere Zahlen berechnen:

• 16 + 1 + ___ + 10 = 34 und wir ergänzen die 7.
• 9 + 8 + ___ + 15 = 34 und wir ergänzen die 2.

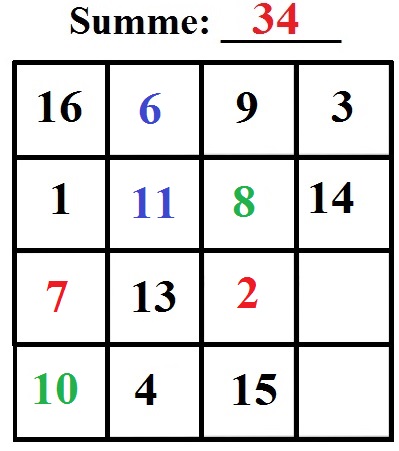
Fehlen rechts noch zwei Zahlen:

• 7 + 13 + 2 + ___ = 34 und wir ergänzen die 12.
• 10 + 4 + 15 + ___ = 34 und wir ergänzen die 5.

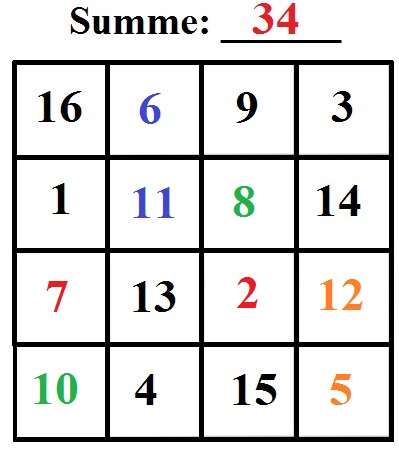
Aufgaben / Übungen magische Quadrate

Aufgabe 1: Bevor wir zum Rechnen kommen eine kurze Frage. Die Summe in allen Zeilen, Spalten und __________ muss gleich sein. Welches Wort fehlt?

• Kanäle
• Diagonalen
• Werten
• ZeilSpalte

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Magisches Quadrat Video

Fragen mit Antworten magische Quadrate