Nenner rational machen (Wurzel)

Wie man einen Nenner rational macht, lernt ihr hier. Folgende Inhalte werden angeboten:

• Eine Erklärung, wie man Nenner rational macht.
• Beispiele wie man aus einem Nenner die Wurzel entfernt.
• Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Umgang mit Brüchen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier gleich an wie man Nenner mit Wurzeln rational macht. Sehr hilfreich ist es, wenn ihr bereits ein bisschen was in der Bruchrechnung kennt und einfache Wurzeln ziehen könnt. Wer in den folgenden Abschnitten etwas nicht versteht, sollte kurz in diese beiden Themen rein sehen.

Rational machen von Nennern

Klären wir zunächst was mit Nenner rational machen gemeint ist:

Sehen wir uns einige Beispiele dazu an wie man den Nenner rational machen und vereinfachen kann.

Beispiel 1: Bruch mit Variablen erweitern

Mache den nächsten Bruch (mit Variablen) mit einer Wurzel im Nenner rational durch Erweiterung.

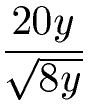
Lösung:

Im Nenner haben wir die Wurzel aus 8y. Um diesen Nenner rational zu machen erweitern wir genau damit. Wir multiplizieren aus diesem Grund daher Zähler und Nenner mit der Wurzel aus 8y. Im Nenner multiplizieren wir die beiden Ausdrücke und es bleibt nur 8y stehen.

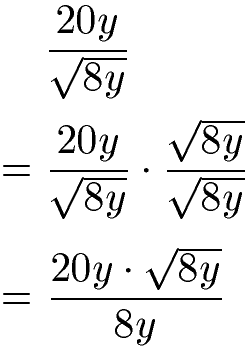
Im Zähler zerlegen wir den Ausdruck unter der Wurzel in 2 · 4 · y. Wir können teilweise die Wurzel ziehen. Die Wurzel aus 4 kann gezogen werden (ergibt 2) und mit den 20y davor multipliziert werden. Im letzten Schritt kann gekürzt werden .

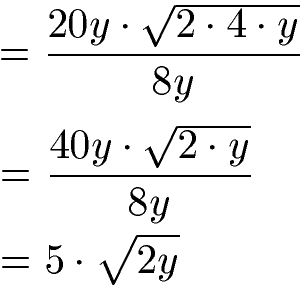
Anzeige:

Nenner rational machen und vereinfachen

In diesem Abschnitt sehen wir uns zwei weitere Beispiele an um die Wurzel im Nenner zu entfernen.

Beispiel 2: Wurzel im Zähler und Nenner

Im Zähler haben wir die Wurzel aus 3 mal Wurzel aus 28 und im Nenner die Wurzel aus 21. Mache den Nenner rational und vereinfache.

Lösung: Wir erweitern mit dem Nenner den Bruch. Im Zähler schreiben wir die Zahlen alle unter eine Wurzel (Wurzelgesetze verwenden) und multiplizieren unter der Wurzel aus. Die Wurzel aus 1764 wird gezogen und ergibt 42. Geteilt durch 21 wird das Ergebnis 2 berechnet.

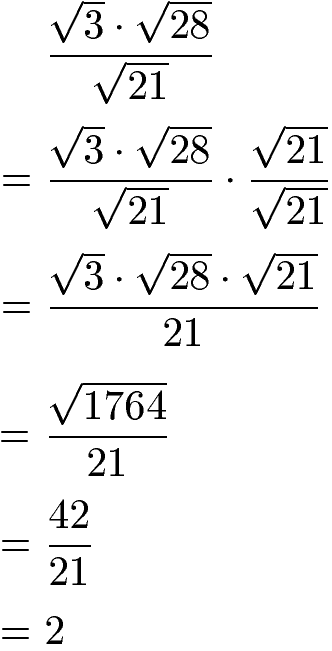
Beispiel 3: Binomische Formel zum Rational machen

Ein weiteres Beispiel soll gerechnet werden. Im Zähler liegt 9x - 15y vor. Im Nenner haben wir die Differenz aus Wurzel von 3x und Wurzel 5y. Wie machen wir den Nenner rational? Dazu verwenden wir die Binomischen Formeln und multiplizieren den Ausgangsbruch mit dem Nenner (wobei das Minus durch Plus ausgetauscht wird wegen Binomischen Formeln). Durch Ausmultiplikation im Nenner wird dieser wurzelfrei. Im Zähler klammern wir vorne eine 3 aus um kürzen zu können.

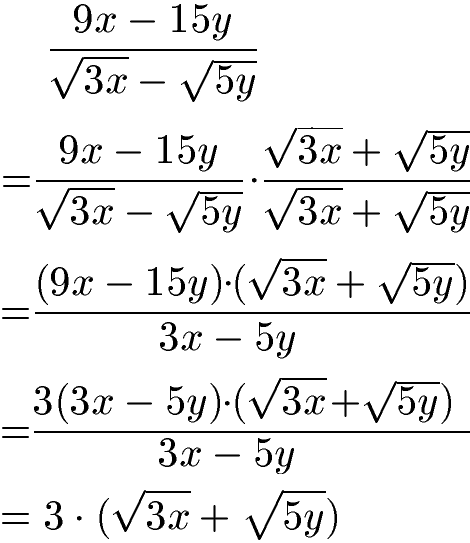
Wurzelrechnung Aufgaben / Übungen

Aufgabe 1: Bevor es Rechenaufgaben gibt ein paar Fragen: Wie nennt man dieses Zeichen?

• Wurzelzeichen
• Quadratwert
• Wurzelwert
• Radikand

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Wurzelrechnung Grundlagen Video

Fragen mit Antworten Nenner rational machen