Punkte in Koordinatensystem eintragen / ablesen

Wie man Punkt in ein Koordinatensystem einträgt sehen wir uns hier an. Dies sind die Themen:

• Eine Erklärung, wie man Punkte einträgt.
• Beispiele wie man Punkte in ebene und räumliche Koordinatensysteme einträgt.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zum Koordinatensystem.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Ihr solltet bereits Koordinatensysteme kennen. Wenn ihr euch mit den Grundlagen beschäftigt, solltet ihr das x-y-Koordinatensystem kennen. Wenn ihr schon etwas weiter seid helfen noch die Grundlagen zum x-y-z Koordinatensystem. Ansonsten sehen wir uns jetzt an wie man Punkte in diese einträgt.

Punkte in ebenes Koordinatensystem eintragen

Wie trage ich einen Punkt in ein Koordinatensystem ein? Beginnen wir mit einem einfachen Beispiel. Es soll ein Punkt in ein ebenes Koordinatensystem eingetragen werden, also in ein Koordinatensystem mit 2 Achsen.

Beispiel 1: Punkt einzeichnen

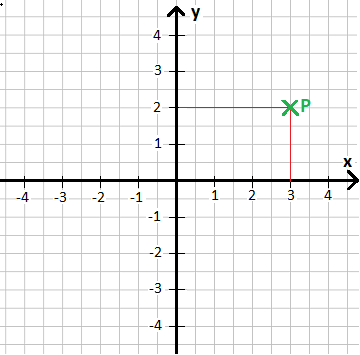
Der Punkt P(3|2) soll in ein x-y Koordinatensystem eingetragen werden. Wo liegt dieser?

Lösung:

Die Angabe P(3|2) bedeutet, dass der Punkt bei x = 3 und y = 2 liegt. Wir gehen daher auf der x-Achse bis zur 3 und von dort um 2 nach oben. Dort liegt der Punkt P.

Beispiel 2: Punkt ablesen

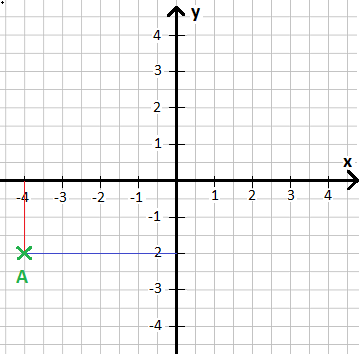
Wo liegt der Punkt im nächsten Koordinatensystem?

Lösung:

Wir gehen auf der Achse bis wir den Punkt erreichen. Dies ist bei x = -4 der Fall. Nach unten erreichen wir den Punkt bei y = -2. Der Punkt liegt damit bei P(-4|-2).

Anzeige:

Punkte in Koordinatensystem mit 3 Achsen

Ein Koordinatensystem kann auch aus 3 Achsen bestehen. Diese werden - gerade in der Schule - oft mit x, y und z bezeichnet. Auch in dieses kann man Punkte eintragen.

Beispiel 3: Punkt einzeichnen

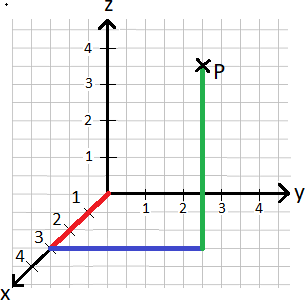
Der Punkt P(3|4|5) soll in ein 3D-Koordinatensystem eingezeichnet werden. Wo liegt dieser?

Lösung:

Dieser Punkt liegt bei x = 3, y = 4 und z = 5. Wir nehmen uns ein Koordinatensystem mit 3 Achsen und schreiben die Achsenbezeichnungen x, y und z an die Achsen. Um den Punkt zu finden, gehen wir die x-Achse um 3 entlang. Danach in y-Richtung um 4 nach rechts und um 5 nach oben.

Wichtig: Es ist nicht möglich einen Punkt aus einem 3D-Koordinatensystem abzulesen, wenn dieses auf einer 2D-Ebene (Papier, Monitor) gezeichnet wurde. In diesem Fall kann man nur raten.

Aufgaben / Übungen Punkt in Koordinatensystem einzeichnen

Aufgabe 1: Wo liegt der Punkt D?

• P (2|5)
• P (-2|3)
• P (5|3)
• P (2|3)

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Koordinatensystem Video

Fragen mit Antworten zu Punkten im Koordinatensystem