Abziehverfahren / Ergänzungsverfahren schriftlich Subtrahieren

Das Abziehverfahren und das Ergänzungsverfahren zum schriftlichen Subtrahieren werden in diesem Artikel behandelt. Dies sehen wir uns an:

• Eine Erklärung, wie das Abziehverfahren und das Ergänzungsverfahren funktionieren .
• Viele Beispiele - auch mit Komma - werden vorgerechnet.
• Aufgaben / Übungen damit ihr beide Varianten lernen könnt.
• Ein Video zum schriftlichen Subtrahieren verschiedenster Zahlen.
• Ein Frage- und Antwortbereich mit typischen Fragen zu diesem Thema.

Hier stellen wir nun das Abziehverfahren dem Ergänzungsverfahren gegenüber. Allgemeine Informationen zu diesem Thema findet ihr auch unter schriftlich Subtrahieren und schriftlich Subtrahieren mit Komma.

Erklärung: Abziehverfahren und Ergänzungsverfahren

Ab der Grundschule werden zwei Verfahren bei der schriftlichen Subtraktion behandelt: Abziehverfahren und Ergänzungsverfahren.

Abziehverfahren:

Fangen wir mit dem Abziehverfahren an. Berechnet werden soll 428 - 207. Die Lösung sieht dann so aus:

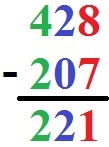
Die Berechnung ist ganz einfach und erfolgt von hinten nach vorne:

• 8 - 7 = 1
• 2 - 0 = 2
• 4 - 2 = 2

Ergänzungsverfahren:

Als Alternative gibt es das Ergänzungsverfahren. Der Unterschied zum Abziehverfahren ist, dass hier umkehrt vorgegangen wird. Hier wird einfach geschaut, was im Ergebnis ergänzt werden muss. Die Berechnung sieht damit so aus:

• 7 + 1 = 8
• 0 + 2 = 2
• 2 + 2 = 4

Ergänzungsverfahren und Abziehverfahren funktionieren auch, wenn die Zahlen ein Komma aufweisen. Die Berechnung sieht dann exakt so aus wie weiter oben schon gezeigt. Nur im Ergebnis muss dann ebenfalls das Komma gesetzt werden.

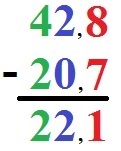
Anzeige:

Beispiele Abziehverfahren / Ergänzungsverfahren

In diesem Abschnitt sollen beide Verfahren für das schriftliche Subtrahieren mit Übertrag noch einmal behandelt werden. Dabei wird das Beispiel 747 - 528 mit dem Abziehverfahren und Ergänzungsverfahren vorgerechnet. Welche Variante ihr im Anschluss selbst verwendet, ist euch überlassen oder wird von Lehrer / Lehrerin vorgegeben. Zunächst einmal das Beispiel, welches im Anschluss erläutert wird.

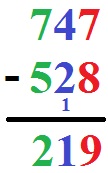
Abziehverfahren:

Zunächst wird die schriftliche Subtraktion mit dem Abziehverfahren berechnet. Wir starten mit der oberen Zahl:

• 7 - 8 funktioniert nicht.
  • Wir wandeln 1 Zehner in 10 Einer um. Aus 7 wird 17.
  • 17 - 8 = 9.
  • Wir schreiben die 9 ins Ergebnis unter dem Strich und notieren uns den Übertrag von 1.
• 4 - 2 = 2 wäre eine falsche Berechnung, da wir hier den Übertrag nicht berücksichtigen würden.
  • Wir ziehen die 1 von der 4 ab, erhalten also 3. Mit 3 - 2 = 1 erhalten wir eine 1 für das Ergebnis.
• 7 - 5 = 2. Wir haben damit noch eine 2 für die Differenz (Ergebnis).

Ergänzungsverfahren:

Dieses Beispiel zur Subtraktion kann auch mit dem Ergänzungsverfahren berechnet werden:

• 8 + ____ = 17.
  • 8 + 9 = 17.
  • Wir schreiben die 9 unter den Strich und die 1 ist der Übertrag.
• 1 + 2 + ___ = 4.
  • 1 + 2 + 1 = 4.
  • Auf dem ___ fehlt uns eine 1, die wir ins Ergebnis übernehmen.
• 5 + ___ = 7
  • 5 + 2 = 7
  • Wir schreiben eine 2 in unser Ergebnis.

Ihr kennt nun das Abziehverfahren und das Ergänzungsverfahren zur schriftlichen Subtraktion. Welches Verfahren ihr benutzt, ist natürlich euch überlassen oder wird vom Lehrer oder der Lehrerin vorgegeben.

Übungsaufgaben Abziehverfahren / Ergänzungsverfahren

Aufgabe 1: Berechne 88 - 67 mit der schriftlichen Subtraktion. Wie lautet das Ergebnis?

• 20
• 22
• 23
• 21

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.

Anzeigen:

Video schriftliche Subtraktion

Abziehverfahren / Ergänzungsverfahren Fragen