Skalarprodukt berechnen: Vektoren, Formel und Definition
Geschrieben von: Dennis RudolphSamstag, 14. März 2020 um 11:23 Uhr
Was das Skalarprodukt ist und wozu man es braucht, lernt ihr hier erklärt. Dies sind die Themen:
- Eine Erklärung, was das Skalarprodukt ist.
- Formeln und Beispiele für das Berechnen von einem Skalarprodukt.
- Aufgaben / Übungen um das Thema selbst zu üben.
- Ein Video zum Skalarprodukt.
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Tipp: Euch sollte bereits klar sein, was ein Vektor überhaupt ist. Falls ihr davon keine Ahnung habt, dann werft bitte erst einen Blick in die Vektoren Grundlagen. Ansonsten ran an das Skalarprodukt.
Skalarprodukt für zwei Vektoren
In der Vektorrechnung bzw. Analytischen Geometrie taucht bei Berechnungen oft das Skalarprodukt auf. Definition Skalarprodukt:
Das Skalarprodukt - auch inneres Produkt gennant - ist eine mathematische Verknüpfung von zwei Vektoren bei der eine Zahl als Ergebnis rauskommt. Ein Malzeichen zwischen zwei Vektoren drückt aus, dass das Skalarprodukt berechnet werden soll. Dabei wird das Malzeichen öfters etwas dicker geschrieben Das Skalarprodukt wird zum Beispiel für die Berechnung eines Winkels zwischen zwei Vektoren verwendet.
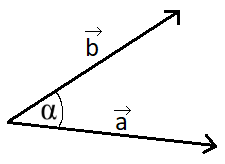
Typischerweise tauchen zwei Formeln in der Mathematik auf im Zusammenhang mit dem Skalarprodukt.
Formel Skalarprodukt ausrechnen
Die erste Formel dient dazu das Skalarprodukt auszurechnen.
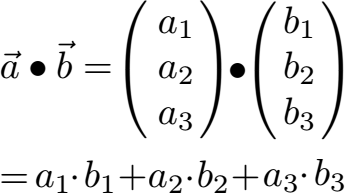
Formel Winkel mit Skalarprodukt
Die zweite Formel wird verwendet um den Winkel zwischen zwei Vektoren zu berechnen.
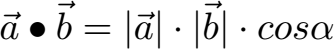
Was diese Formel bedeutet und wie man sie anwendet lernt ihr unter Skalarprodukt Winkel berechnen.
Anzeige:
Anzeigen:
Skalarprodukt berechnen
Sehen wir uns zwei Beispiele an wie man das Skalarprodukt im Raum und in der Ebene ausrechnet und was das Ergebnis bedeutet.
Beispiel 1: Skalarprodukt im Raum
Sehen wir uns einmal eine einfache Berechnung des Skalarproduktes an. Dazu bilden wir das Skalarprodukt zweier räumlicher Vektoren. Verfolgt einfach die Berechnung Zeile für Zeile.
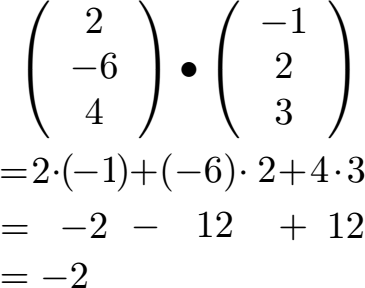
Hinweis: Ist das Skalarprodukt zwei Vektoren kleiner als 0 wie in diesem Beispiel dann ist der Winkel zwischen den Vektoren größer als 90 Grad. Wir sehen uns dies noch genauer an unter Skalarprodukt Winkel berechnen.
Beispiel 2: Skalarprodukt Null
Wir haben zwei Vektoren in der Ebene, in rot und grün eingezeichnet. Ermittel die Vektoren und berechne das Skalarprodukt.
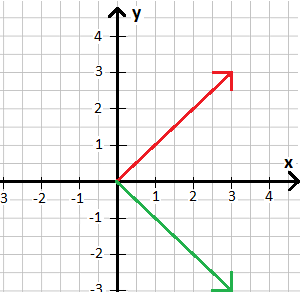
Lösung:
Beide Vektoren starten im Ursprung. Der rote Vektor endet bei x = 3 und y = 3. Der grüne Vektor endet bei x = 3 und y = -3. Damit haben wir beide Vektoren und können ganz einfach Zeile für Zeile das Skalarprodukt beginnen zu rechnen.
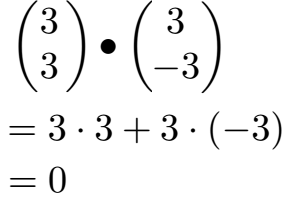
Das Ergebnis ist eine 0.
Merke: Eine Null beim Skalarprodukt bedeutet, dass die beiden Vektoren senkrecht zueinander stehen, also der Winkel zwischen den Vektoren 90 Grad beträgt.
Aufgaben / Übungen Skalarprodukt
Anzeigen:Video mit Skalarprodukt
Erklärung und Beispiele
In diesem Video beschäftigen wir uns mit den Grundlagen der Vektorrechnung. Dies sind die Themen:
- Vektor Addition mit Beispiel
- Subtraktion Vektoren mit Aufgabe
- Was ist ein Skalarprodukt?
- Beispiel Skalarprodukt
Tipp: Versucht die Beispiele noch einmal selbst nachzurechnen.
Nächstes Video »
Fragen mit Antworten zum Skalarprodukt
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zum Skalarprodukt an.
F: Was ist das Skalarprodukt zweier Vektoren? Was sagt uns das Skalarprodukt?
A: Das Skalarprodukt zweier Zahlen ist erst einmal eine Zahl ohne Maßeinheit. Die Zahl ist im Prinzip ein Maß für den Winkel zwischen den beiden Vektoren. Wie man diesen Winkel berechnet lernt ihr unter Skalarprodukt Winkel berechnen.
F: Wann ist ein Skalarprodukt 0?
A: Das Skalarprodukt zweier Vektoren ist 0 wenn die beiden Vektoren in einem rechten Winkel (90 Grad) zueinander stehen.
F: Zu den Rechenregeln. Ist das Skalarprodukt kommutativ oder distributiv?
A: Das Skalarprodukt ist sowohl kommutativ als auch distributiv. Dies ist auch logisch. Das Skalarprodukt ist ein Maß für den Winkel zwischen beiden Vektoren. Welchen Vektor ich bei der Berechnung zuerst nehme hat auf die Winkelgröße keinen Einfluss.
F: Welche Themen sollte ich mir als nächstes ansehen?
A: Wir arbeiten aktuell an diesen Themen und werden sie nach der Veröffentlichung hier verlinken:
- Unterschied Ortsvektor und Richtungsvektor
- Betrag / Länge eines Vektors
- Rechnen mit Vektoren
- Vektoren addieren
- Vektoren subtrahieren
- Mittelpunkt einer Strecke
- Vektorprodukt / Kreuzprodukt
- Spatprodukt
- Abstand Punkt zu Gerade
- Abstand paralleler Geraden
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
