Skalarprodukt Winkel zwischen Vektoren mit Formel

Wie man mit dem Skalarprodukt den Winkel zwischen zwei Vektoren berechnet, lernt ihr hier. Dies sind die Themen:

• Eine Erklärung, wie man das Skalarprodukt nutzt.
• Formeln und Beispiele für die Rechnung mit dem Skalarprodukt.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zum Skalarprodukt.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Um die Winkel zwischen zwei Vektoren zu berechnen, benötigt man die Länge von einem Vektor uns das Skalarprodukt. Wir werden beides hier noch einmal behandeln soweit benötigt. Wer dies ausführlicher noch lernen möchte wirft einen Blick in Länge eines Vektors und Skalarprodukt.

Skalarprodukt: Winkel zwischen zwei Vektoren

Eine Anwendung vom Skalarprodukt besteht darin den Winkel zwischen zwei Vektoren zu berechnen.

Die Formel um die Berechnung durchzuführen wird den einen oder anderen Schüler oder Studenten etwas erschrecken. Natürlich muss die Formel der Vollständigkeit wegen angegeben werden.

Um den Winkel zwischen zwei Vektoren zu berechnen muss man diese Formel natürlich nach dem Winkel Alpha umstellen.

Formel Skalarprodukt nach Winkel umgestellt:

Dies sagt die Formel:

• Links haben wir den Cosinus von Alpha. Bei der Berechnung des Winkels müsst ihr den Taschenrechner auf DEG stellen. Dies sehen wir auch gleich bei den Beispielen.
• Im Zähler haben wir das Skalarprodukt der beiden Vektoren.
• Im Nenner müssen wir die Länge jedes Vektors berechnen und die beiden miteinander multiplizieren.

Im nächsten Abschnitt sehen wir uns Beispiele an.

Anzeige:

Winkel mit Skalarprodukt Beispiele

Sehen wir uns an wie man die Winkelberechnung in Ebene und Raum durchführt.

Beispiel 1: Winkel Raum

Wie groß ist der Winkel zwischen diesen beiden Vektoren?

Lösung:

Im ersten Schritt bilden wir das Skalarprodukt. Die allgemeine Formel lautet:

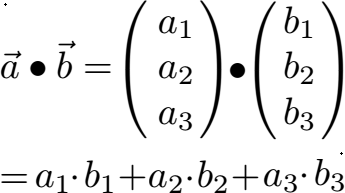
Wir setzen die Zahlen der beiden Vektoren ein und erhalten 32 als Ergebnis:

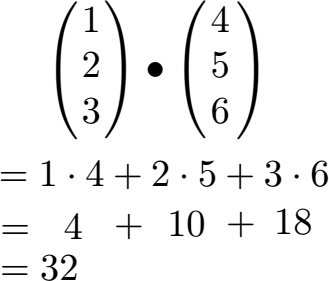
Fehlt uns noch die Länge der beiden Vektoren. Dazu quadrieren wir unter der Wurzel die einzelnen Zahlen.

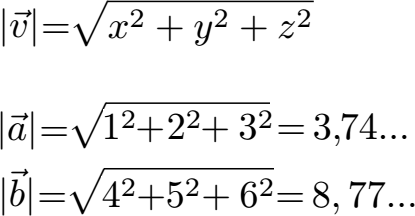
Das Skalarprodukt und die Längen der beiden Vektoren setzen wir in die Formel ein. Um Alpha zu berechnen müssen wir den Taschenrechner auf DEG stellen. Mit arccos(0,9756) erhalten wir einen Winkel von etwa 13 Grad.

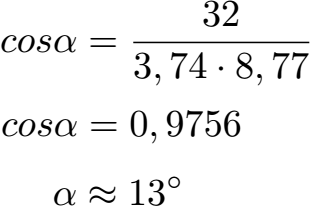
Beispiel 2: Winkel Ebene

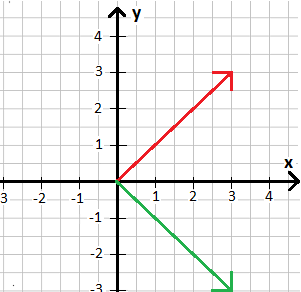
Wir haben zwei Vektoren in der Ebene, welche im nächsten Bild eingezeichnet sind. Berechne den Winkel mit dem Skalarprodukt.

Lösung:

Beide Vektoren starten im Ursprung des Koordinatensystems. Der rote Vektor endet bei x = 3 und y = 3. Der grüne Vektor endet bei x = 3 und y = -3. Das Skalarprodukt bilden wir, indem wir in jeder Zeile multiplizieren und dazwischen ein Pluszeichen setzen.

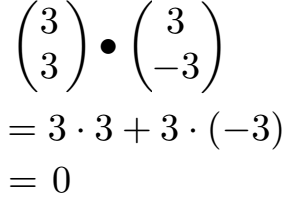
Wir berechnen noch die Länge eines Vektors. Oder besser gesagt: Wir berechnen die Länge beider Vektoren. Unter einer Wurzel quadrieren wir dazu jede Zahl des Vektors und addieren diese.

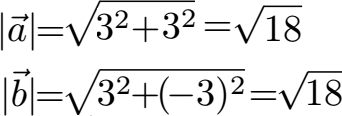
Damit können wir den Winkel zwischen den beiden Vektoren berechnen. Wichtig: Taschenrechner auf DEG stellen und arccos (0) eingeben. Erst danach den arccos von 0 berechnen.

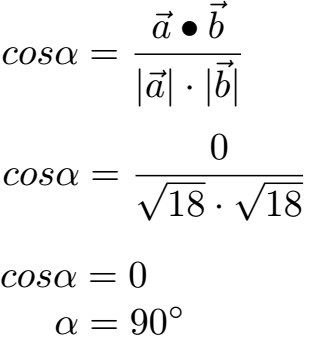
Aufgaben / Übungen Skalarprodukt

Aufgabe 1:

In diesem Bereich erhaltet ihr die Möglichkeit das Skalarprodukt zu üben. Da einige Schüler und Studenten jedoch bereits an einfachen Fragen scheitern, gibt es auch bei uns Fragen zum Thema.

• Was erhält man wenn man Skalarprodukt ausrechnet?

• Eine Länge
• Eine Zahl
• Ein Vektor
• Eine Matrix

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video mit Skalarprodukt

Fragen mit Antworten Skalarprodukt Winkelberechnung