Länge (Betrag) eines Vektors berechnen

Wie man den Betrag (= Länge) eins Vektors berechnet, lernt ihr hier. Dies sind die Themen:

• Eine Erklärung, wie man die Länge von einem Vektor berechnet.
• Beispiele für Vektorlängen in Ebene und Raum.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Längenberechnung von Vektoren.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich, wenn ihr bereits wisst, was ein Koordinatensystem ist und was ein Vektor ist. Wer davon noch keine Ahnung hat, wirft einen Blick auf x-y-z Koordinatensystem und Vektoren Grundlagen.

Betrag eines 2D-Vektors

Vektoren gibt es in der Ebene (2D) und im Raum (3D). Starten wir mit der Länge eines ebenen Vektors. Dazu haben wir einen Vektor (erkennt man an dem Pfeil über dem v) mit x und y. Die Länge dieses Vektors berechnet man in dem man die Wurzel aus x² + y² zieht. Der Betrag des Vektors erkennt man an der Schreibweise mit zwei Betragsstrichen.

Länge ebener Vektor Formel

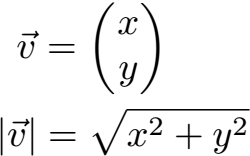
Beispiel 1: Länge ebener Vektor

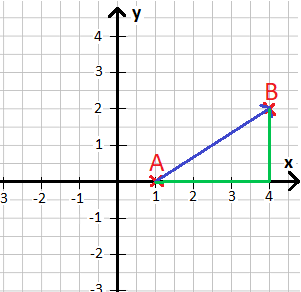
Wie lange ist der blaue Vektor?

Lösung:

Der Punkt A liegt bei x = 1 und y = 0, also A (1|0). Der Punkt B liegt bei x = 4 und y = 2, also B (4|2). Um von A nach B zu kommen müssen wir in x-Richtung um 3 nach rechts und in y-Richtung um 2 nach oben gehen. Daher ist unser Vektor dieser hier:

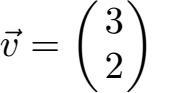
Die Länge des Vektors berechnen wir mit der Formel von weiter oben.

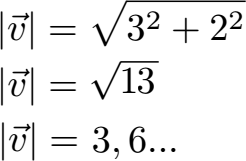
Länge Vektor Herleitung

Die Herleitung der Vektorlänge ist relativ einfach. Wie man dem gezeichneten Vektor ansehen kann, sieht man dort ein rechtwinkliges Dreieck. Daher kann man auch den Satz des Pythagoras nutzen. Die beiden grünen Linien sind dabei die Katheten und die Länge des blauen Vektors die Hypotenuse. Daher nehmen wir die Formel hinter dem Satz des Pythagoras:

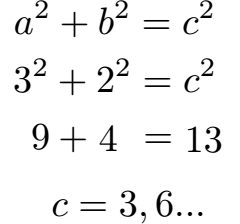
Anzeige:

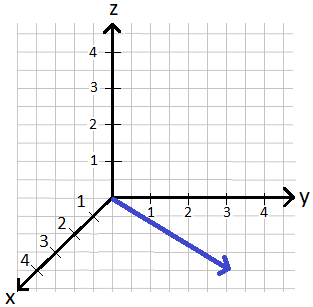
Länge eines 3D-Vektors

Ein Vektor kann nicht nur in der Ebene, sondern auch im Raum vorkommen. Die nächste Grafik zeigt einen beliebigen 3D-Vektor in einem x-y-z-Koordinatensystem.

Formel Länge Vektor im Raum (3D):

Hat man einen dreidimensionalen Vektor mit x, y und z berechnet sich der Betrag (Länge) des Vektors nach der folgenden Formel.

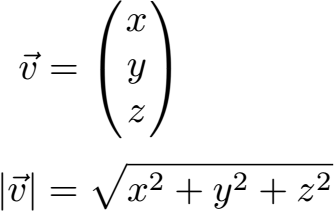
Beispiel 2: Betrag Vektor im Raum berechnen

Sehen wir uns noch ein Beispiel mit Zahlen an. Wie lange ist ein Vektor mit x = 1, y = 2 und z = 3?

Lösung:

Wir schreiben den Vektor auf und setzen die Zahlen in die Formel für die Betragsberechnung des Vektors ein.

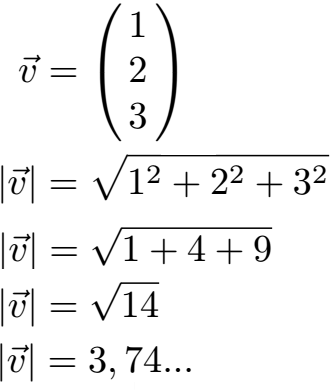
Aufgaben / Übungen Vektoren Länge

Aufgabe 1: In diesem Bereich könnt ihr den Betrag von Vektoren üben. Leider ist es oft so, dass viele Schüler und auch Studenten bereits an Begriffen zur Vektorrechnung scheitern. Daher bieten wir hier neben Aufgaben mit Zahlen auch noch ein paar Fragen zum Thema an.

• Was berechnet man mit dem Betrag eines Vektors?

• Der Winkel zwischen drei Vektoren
• Die Länge des Vektors
• Der Einheitswinkel
• Die Vektorumkehr

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Länge eines Vektors

Fragen mit Antworten: Betrag eines Vektors