Umfang Dreieck

Wie man den Umfang von einem Dreieck berechnet, zeigen wir euch hier. Dies sehen wir uns an:

• Eine Erklärung und Formeln, wie man den Umfang von einem Dreieck berechnet.
• Viele Beispiele zur Berechnung, auch mit Einheiten.
• Aufgaben / Übungen zum Umfang eines Dreiecks.
• Ein Video zum Thema.
• Ein Frage- und Antwortbereich zum Dreiecksumfang.

Ein kleiner Tipp zum Start: Wer mit den folgenden Inhalten noch Probleme hat, dem fehlen vielleicht ein paar Vorkenntnisse. In diesem Fall bitte einen Blick auf die Artikel Meter, Dezimeter und Zentimeter werfen und auch auf Was sind Variablen.

Erklärung Umfang Dreieck

Ein Dreieck hat - wie der Name schon sagt - drei Ecken. Ein Dreieck kann einen rechten Winkel aufweisen, muss es aber nicht. Wir beschäftigen uns hier mit den Umfängen verschiedener Dreiecksarten. Sehen wir uns dazu einmal ein beliebiges Dreieck an. Die Seiten werden dabei zur besseren Übersicht mit unterschiedlichen Farben markiert. An jede Seite wird eine Variable (also ein Buchstabe) geschrieben.

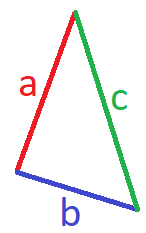
Das a steht dabei für die Länge der roten Seite, das b für die Länge der blauen Seite und das c für die Länge der grünen Seite.

Formel Umfang Dreieck:

Die einfache Formel zur Berechnung des Umfangs eines Dreiecks lautet damit:

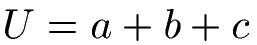
Diese Formel gilt in jedem Dreieck, egal ob ein rechter Winkel vorhanden ist oder nicht.

Beispiel 1:

Sehen wir uns ein einfaches Beispiel an. Die rote Seite sei 14 cm lang, die blaue Seite 10 cm und die grüne Seite 16 cm. Wie groß ist der Umfang des Dreiecks?

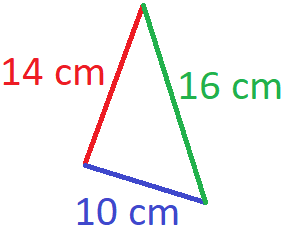
Lösung:

Wir müssen einfach die drei Angaben in Zentimeter addieren um den Umfang zu erhalten:

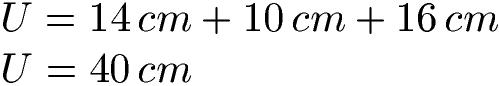
Wir erhalten damit einen Umfang von 40 Zentimeter.

Anzeige:

Beispiele Umfang Dreieck

In diesem Abschnitt sollen weitere Beispiele zum Umfang eines Dreiecks berechnet werden. Dabei geht es auch um ein rechtwinkliges Dreieck, inklusive dem Rechnen mit einer Unbekannten. Darüber hinaus sehen wir uns an, wie man mit verschiedenen Einheiten umgeht (und diese umrechnet).

Beispiel 2:

Wir haben ein rechtwinkliges Dreieck. Links unten - also da wo a und b aufeinander stoßen - haben wir einen rechten Winkel. Darüber hinaus haben wir noch die Länge c. Die Länge c ist am Längsten. Das Dreieck sieht dann zum Beispiel so aus:

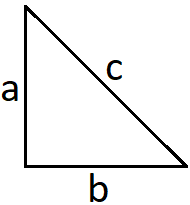
Nehmen wir folgendes an: Die Länge a sei 9 cm und b sei 8 cm. Wir haben damit ein Dreieck mit einer Unbekannten und sollen diese berechnen. Eine Seite fehlt damit. Wie groß ist der Umfang des Dreiecks?

Lösung:

Um den Umfang zu berechnen, muss man a + b + c rechnen. Wir kennen c jedoch nicht. Daher müssen wir die Länge von c zunächst berechnen. Wir haben hier ein Dreieck mit einem rechten Winkel. Daher dürfen wir den Satz des Pythagoras verwenden um c zu berechnen. Die Gleichung zum Satz des Pythagoras lautet:

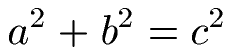
Wir setzen hier a = 9 cm und b = 8 cm ein und berechnen damit die Länge c, auch Hypotenuse genannt.

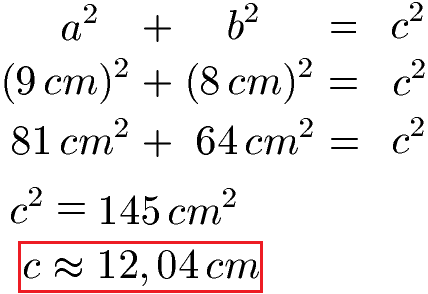
Wir wissen nun wie lange die drei Seiten sind. Für den Umfang müssen wir a, b und c noch addieren.

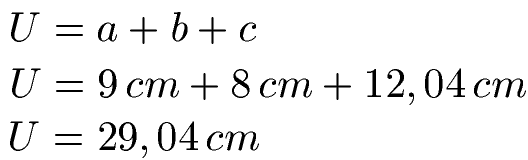
Beispiel 3:

Im dritten Beispiel sollen verschiedene Maßeinheiten und Kommazahlen mit berücksichtigt werden. Nehmen wir wieder ein Dreieck. Für die Berechnung sind die Längen der Seiten 60 Zentimeter sowie 0,8 Meter und 13,4 Zentimeter. Wie groß ist der Umfang?

Lösung:

Wir haben zwei Angaben in Zentimeter und eine Angabe in Meter. Da wir alle Angaben in einer Einheit brauchen, rechnen wir alles auf Zentimeter um. Dabei entsprechen 0,8 Meter nun 80 Zentimeter. Im Anschluss rechnen wir einfach a + b + c um den Umfang zu bekommen.

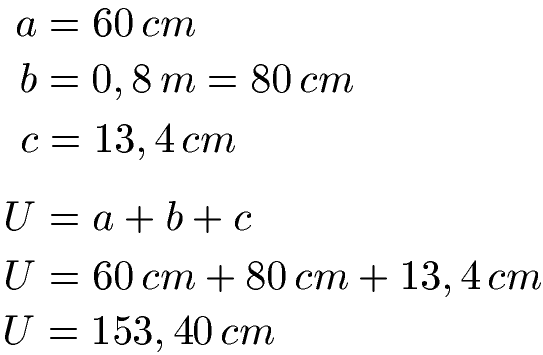
Dreieck Umfang Übungsaufgaben

Aufgabe 1: Die drei Seiten eines Dreiecks sind 5 cm, 10 cm und 8 cm lang. Wie groß ist der Umfang?

• 28 cm
• 25 cm
• 23 cm
• 15 cm

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Umfang und Fläche Dreieck

Fragen mit Antworten Umfang Dreieck