Zuordnungen: Erklärung mit Beispielen

Was eine Zuordnung ist und wozu man sie braucht, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung was eine Zuordnung ist.
• Beispiele für Zuordnungen, auch proportional und antiproportional.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Dreisatz.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns gleich an, was eine Zuordnung ist. Als Vorkenntnisse hilft es, wenn ihr wisst, was eine Gleichung ist. Wer davon noch keine Ahnung hat sieht bitte in Gleichung auflösen rein.

Erklärung Zuordnung

In der Mathematik - und auch im echten Leben - ordnet man oft zwei Ding einander zu:

• Ein Kind wird seiner Mutter zugeordnet.
• Ein Auto wird einer Garage zugeordnet.
• Einem Brötchen wird ein Preis zugeordnet.

Beispiel 1: Zuordnung Brötchen zu Preis

Ein Brötchen kostet 50 Cent. Zwei Brötchen kosten das Doppelte und so weiter. Man kann daher der Anzahl der Brötchen jeweils einen Preis zuordnen.

• 1 Brötchen kostet 0,50 Euro.
• 2 Brötchen kosten 1,00 Euro.
• 3 Brötchen kosten 1,50 Euro.
• 4 Brötchen kosten 2,00 Euro.

Man kann dies mit zwei Mengen darstellen. Jedem Element der ersten Menge (Anzahl) wird ein Element der zweiten Menge (Preis) zugeordnet. Ein Pfeil zeigt hier die eindeutige Zuordnung:

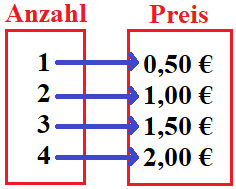
Man kann diesen Zusammenhang auch mit einer Gleichung darstellen. Dabei muss man die Anzahl der Brötchen (x) mit 0,50 Euro multiplizieren. Dadurch erhalten wir den Gesamtpreis (y). Die Gleichung sieht so aus:

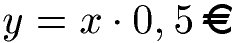
Anzeige:

Dreisatz Zuordnung proportional / antiproportional

Dem einen oder anderen mag der Dreisatz vielleicht nichts sagen. Daher sehen wir uns erst einmal an, was man darunter versteht:

Der Dreisatz ist ein Verfahren aus der Mathematik, bei dem man aus drei gegebenen Werten einen vierten Wert berechnen kann. Dabei müssen die Werte in einem gewissen Verhältnis zueinander stehen. Der Dreisatz ist ein Verfahren, welches in der Schulmathematik unterrichtet wird.

Beispiel 2: proportionaler Dreisatz:

• 1 Tafel Schokolade kostet 1 Euro.
• 2 Tafeln Schokolade kosten 2 Euro.
• 3 Tafeln Schokolade kosten 3 Euro.

Dies ist auch eine Zuordnung, denn man kann die Anzahl der Tafeln dem Preis zuordnen. Verdoppelt man die Anzahl, verdoppelt sich der Preis. Verdreifacht man die Anzahl, dann verdreifacht sich der Preis. Und so weiter. So etwas bezeichnet man als proportionalen Dreisatz. Es gilt: Je mehr, desto mehr.

Beispiel 3: antiproportionaler Dreisatz

Nehmen wir ein anderes Beispiel zum Dreisatz: 2 Pumpen brauchen 3 Tage um eine Lagerhalle von Wasser zu befreien. Wie viele Pumpen werden benötigt um es in 12 Stunden zu schaffen?

Lösung:

Es sollte klar sein, dass wenn weniger Zeit zum Pumpen da ist, dass mehr Pumpen benötigt werden. Daher erkennt man, dass man keinen proportionalen Zusammenhang hat. Sondern das Gegenteil: Einen antiproportionalen Zusammenhang.

In die erste Zeile schreiben wir die Startinformationen: In 3 Tagen packen es 2 Pumpen.

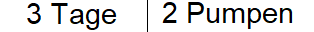
Um von 3 Tage auf 1 Tag zu kommen, teilen wir auf der linken Seite durch 3. Bei proportionalen Rechenaufgaben macht man auf der rechten Seite genau das Gleiche. Wir haben hier jedoch eine antiproportionale Zuordnung. Daher teilen wir auf der rechten Seite nicht durch 3, sondern multiplizieren mit 3. Wir kommen damit zu dem Ergebnis, dass 6 Pumpen die Lagerhalle an einem einzigen Tag frei Pumpen könnten.

Wir interessieren uns jedoch bei dieser Aufgabe dafür, wie viele Pumpen man braucht um alles in einem halben Tag (12 Stunden) zu schaffen. Um von einem ganzen Tag auf einen halben Tag zu kommen, müssen wir noch einmal durch 2 dividieren. Auch dabei gilt: Wir haben einen antiproportionalen Dreisatz. Daher müssen wir rechts nicht durch 2 dividieren, sondern mit 2 multiplizieren.

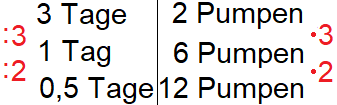
Fazit: Mit 12 Pumpen gelingt es die Lagerhalle in 12 Stunden von Wasser zu befreien (sieht man von Restfeuchtigkeit ab).

Zuordnung Dreisatz Übungen

Aufgabe 1: Bevor wir rechnen kurz ein paar Wissensfragen. Wie nennt man das Gegenteil von proportional beim Dreisatz?

• antiproportional
• mixproportional
• unproportional
• gegenproportional

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Zuordnung und Dreisatz

Fragen mit Antworten zur Zuordnung