Spezifischer Widerstand

Mit dem spezifischen Widerstand befassen wir uns in diesem Artikel. Kurzfassung der Inhalte:

• Eine Erklärung, was der spezifische Widerstand ist und eine Tabelle dazu.
• Einige Beispiele zum Rechnen mit dem spezifischen Widerstand.
• Aufgaben / Übungen damit ihr alles selbst üben könnt.
• Ein Video zum spezifischen Widerstand.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Erklärung spezifischer Widerstand

Wie groß ein elektrischer Widerstand ist, hängt vom verwendeten Material ab, wie lang und dick dieses ist und welche Temperatur herrscht. Damit sind wir recht schnell beim spezifischen elektrischen Widerstand - kurz auch spezifischer Widerstand genannt - oder auch Resistivität.

Der spezifische Widerstand gibt an, welchen elektrischen Widerstand ein Leiter aus einem Material besitzt, welcher 1 m lang ist und dabei eine durchgehende Fläche von 1 mm² aufweist. Grundsätzlich ist dieser spezifische Widerstand abhängig von der Temperatur.

Zum Rechnen in der Physik geht man jedoch oftmals davon aus, dass die Temperatur konstant ist. In diesem Fall gilt die folgende Formel / Gleichung um den Widerstand zu berechnen:

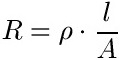
Dabei ist:

• "R" der elektrische Widerstand des Leiters
• "ρ" der spezifische Widerstand
• "l" die Länge des Leiters
• "A" ist die Fläche (Querschnittsfläche) des Leiters

Möchte man den spezifischen Widerstand direkt berechnen, dann stellt man die Formel nach dem Rho (ρ) um:

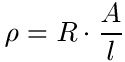
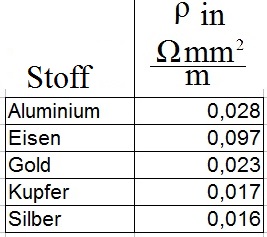
Bevor wir uns noch Beispiele mit Zahlen und Einheiten ansehen erst einmal eine Tabelle mit typischen Werten für verschiedene Stoffe. Es gibt natürlich noch deutlich umfangreichere Tabellen, aber um ein bisschen damit Rechnen zu lernen langt diese. Die Tabelle für Aluminium, Eisen, Gold, Kupfer und Silber.

Anzeige:

Beispiele spezifischer Widerstand

Um den Umgang mit dem spezifischen Widerstand zu erlernen helfen oftmals eine Reihe an Beispielen.

Beispiel 1:

Im ersten Beispiel nehmen wir an, dass wir eine Leitung haben, die 0,5 km lang ist und aus Kupfer besteht. Die Fläche / Querschnittsfläche sei 900 Quadratmillimeter. Wie groß ist der Widerstand dieser Leitung?

Lösung:

Im Aufgabentext steht, dass die Leitung aus Kupfer besteht, daher entnehmen wir der Tabelle ρ = 0,017 Ohm mal Millimeterquadrat pro Meter ablesen. Bei dieser Angabe sehen wir auch, dass wir als Einheiten noch Millimeterquadrat und Meter brauchen für die restlichen Daten. Daher setzen wir die Länge nicht in Kilometer ein, sondern rechnen diese auf 500 Meter um. Die 900 Quadratmillimeter für die Querschnittsfläche können wir direkt verwenden. Wir setzen ein, kürzen und erhalten den Widerstand der Leitung.

Beispiel 2:

Im zweiten Beispiel soll es umgekehrt laufen. Berechnet werden soll der spezifische Widerstand ρ. Der Leiter hat einen Widerstand von 0,0094 Ohm und sei 500 Meter lang. Die Querschnittsfläche sei 900 Quadratmillimeter.

Aufgaben / Übungen spezifischer Widerstand

Aufgabe 1: Bevor wir rechnen ein paar kurze Fragen. Das Widerstandsgesetz lautet:

Wofür steht das "R"?

• der Querschnitt
• der spezifische elektrische Widerstand
• der elektrische Widerstand
• die Länge des Leiters

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Videos spezifischer Widerstand

Fragen und Antworten spezifischer Widerstand