Bruchgleichungen / Gleichungen mit Brüche
Geschrieben von: Dennis RudolphSonntag, 08. April 2018 um 12:29 Uhr
Wie man Bruchgleichungen - also Gleichungen mit Brüche - löst, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, wie man Bruchgleichungen lösen kann.
- Beispiele zum Lösen von Gleichungen mit Brüchen.
- Aufgaben / Übungen damit ihr dies selbst üben könnt.
- Ein Video zu Bruchgleichungen.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Wir sehen uns gleich Bruchgleichungen an, also ein Mix aus Gleichungen und Brüchen. Daher ist es unglaublich hilfreich, wenn ihr bereits Gleichungen lösen könnt und ihr auch wisst, wie die Bruchrechnung funktioniert. Noch keine Ahnung davon? Dann bitte die beiden Links anklicken und nachlesen.
Erklärung Bruchgleichungen
Was ist überhaupt eine Bruchgleichung? Eine kurze Definition:
Eine Bruchgleichung ist eine Gleichung, bei der mindestens ein Bruch vorkommt. Dieser enthält eine Variable - oftmals x genannt - welche im Nenner eines oder mehrerer Brüche vorkommt. Ziel in der Mathematik ist es meistens die Gleichung nach dieser Variablen umzuformen.
Wir sehen uns gleich einige Beispiele dazu an, jedoch zuerst ein paar Regeln und Tipps zu Bruchgleichungen:
- Durch Null darf nicht geteilt werden.
- Es darf nicht mit Null multipliziert werden.
- Ein Nenner wird beseitigt, in dem man mit diesem multipliziert.
- Ziel ist es nach der Variablen aufzulösen, also x = ____ zu erhalten.
Beispiel 1:
Beginnen wir mit einem ganzen einfachen Beispiel. Die nächste Gleichung hat einen Bruch und soll nach der Variablen x aufgelöst werden.
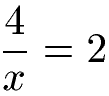
Lösung:
1. Schritt:
Durch Null darf nicht geteilt werden. Daher darf der Nenner nicht 0 werden. In diesem Fall ist das ganz einfach, denn x = 0 ist nicht erlaubt. Was nicht erlaubt ist, schreiben wir in eine Definitionsmenge. Diese sieht für dieses Beispiel so aus:
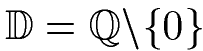
2. Schritt:
Um nach x aufzulösen, müssen wir das x aus dem Nenner herausbekommen. Dies ist hier ganz einfach, denn wir können einfach mit x multiplizieren. Die Rechenschritte schreiben wir jeweils hinter einen Strich. Auf der linken Seite der Gleichung bleibt damit nur die 4 stehen und rechts erhalten wir 2 · x, kurz 2x. Die 2 vor dem x stört noch, denn wir möchten nur x haben. Um eine Multiplikation mit 2 umzukehren, teilen wir durch 2. Dadurch erhalten wir x = 2.
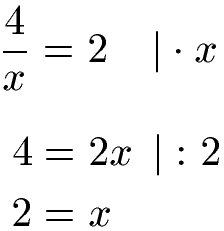
3. Schritt:
Wir müssen noch prüfen, ob x = 2 erlaubt ist. Dies ist der Fall, denn wir haben über die Definitionsmenge nur x = 0 als nicht erlaubt berechnet. Wir dürfen damit unsere Lösung x = 2 in die Bruchgleichung einsetzen. Das Ergebnis unserer Berechnung schreiben wir in die Lösungsmenge:
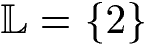
Soweit ein einfaches Beispiel zur Einführung. Es wird Zeit für ein paar schwerere Fälle.
Anzeige:
Anzeigen:
Beispiele Gleichungen mit Brüche
Machen wir die Bruchgleichungen etwas schwieriger.
Beispiel 2:
Wir haben die nächste Gleichung mit Bruch. Genauer gesagt mit zwei Brüchen. Berechne den Definitionsbereich, löse nach der Variablen x auf und gibt die Lösungsmenge an.
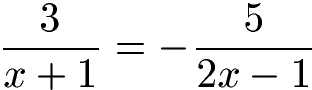
1. Schritt:
Durch Null darf nicht geteilt werden! Daher sehen wir uns beide Brüche an, denn beide Brüche haben eine Variable im Nenner. Um die Zahlen zu ermitteln, welche nicht eingesetzt werden dürfen (Definitionsmenge), müssen wir damit beide Nenner gleich Null setzen und jeweils x berechnen:
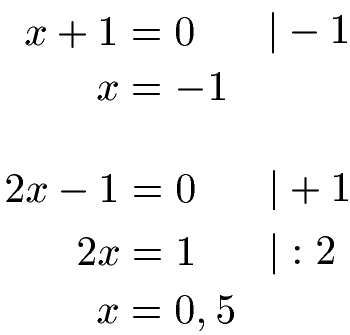
Wir dürfen x = -1 und x = 0,5 nicht einsetzen, denn einer der beiden Nenner würde jeweils Null werden. Damit können wir unseren Definitionsbereich aufschreiben:
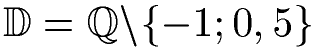
2. Schritt:Im zweiten Schritt soll x berechnet werden. Dazu müssen wir die beiden Nenner beseitigen und nach x auflösen. Werft erst einmal einen Blick auf die Berechnung, welche im Anschluss Schritt für Schritt erklärt wird.
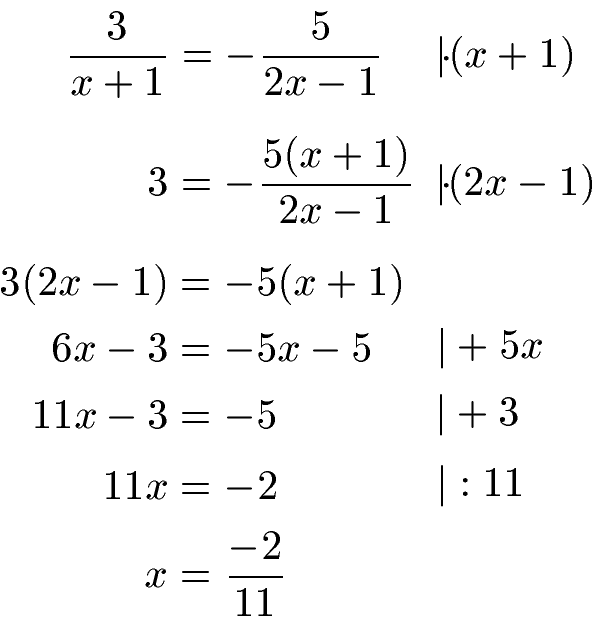
Um einen Nenner los zu werden, müssen wir mit diesem multiplizieren. Das heißt um (x + 1) im Nenner zu beseitigen, multiplizieren wir beide Seiten der Bruchgleichung mit (x + 1). Links fällt dies damit weg und rechts kommt dies - mit Klammern - in den Zähler. Im Anschluss machen wir dies auch für (2x -1) und multiplizieren beide Seiten der Gleichung mit (2x - 1). Dadurch fällt dies auf der rechten Seite raus und auf der linken Seite kommt es - ebenfalls in Klammern - in den Zähler. Aus einer Gleichung mit Brüchen haben wir eine Gleichung ohne Brüche gemacht.
Wir multiplizieren beide Seiten der Gleichung aus: Auf der linken Seite 3 · 2x = 6x und 3 · (-1) = -3. Auf der rechten Seite (-5) · x = -5x und (-5) · 1 = - 5. Im Anschluss müssen wir alles mit x auf eine Seite der Gleichung schaffen und alles ohne x auf die andere Seite. Dies erreichen wir, indem wir zunächst +5x auf beiden Seiten rechnen. Auf der linken Seite erhalten wir 6x + 5x = 11x und rechts fallen die -5x weg. Danach rechnen wir +3 auf beiden Seiten wodurch die -3 links wegfallen und rechts erhalten wir - 5 + 3 = -2. Um von 11 · x (kurz 11x) auf x zu kommen, müssen wir noch durch 11 teilen.
Tipp: Wer beim Ausrechnen der Klammern noch Probleme hat, kann gerne noch in Gleichungen mit Klammern reinsehen.
3. Schritt:
Wir erhalten x = -2 : 11 als Lösung. Diesen Wert für x finden wir nicht in der Definitionsmenge, daher haben wir hier die Lösung für die Lösungsmenge gefunden.
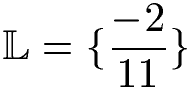
Weitere Beispiele findet ihr im Aufgabenbereich. Zum Beispiel eine Bruchgleichung mit Quadrat im Nenner oder ein weiteres Beispiel mit zwei Brüchen.
Aufgaben / Übungen Gleichung mit Brüche
Anzeigen:Video Bruchgleichungen
Beispiele und Erklärungen
Im nächsten Video wird erklärt, was eine Bruchgleichung ist und wie man die entsprechenden Gleichungen mit Brüchen Schritt für Schritt lösen kann. Zum besseren Verständnis werden dazu Beispiele mit Zahlen und Variablen vorgerechnet und erläutert.
Nächstes Video »
Fragen mit Antworten Bruchgleichung
In diesem Abschnitt geht es um typische Fragen mit Antworten rund um Gleichungen mit Brüchen.
F: Kann man Bruchgleichungen auch mit einem Hauptnenner lösen?
A: Das Beispiel Nr. 2 hätte man auch mit einem Hauptnenner lösen können. Man hätte damit nicht nacheinander (2x -1) und dann mit (x + 1) multiplizieren können, sondern direkt auch mit (2x -1)(x + 1). Damit tun sich jedoch viele Mathematik-Lernende schwer, daher haben wir es oben Stück für Stück gerechnet.
F: Was muss ich beim Umformen der Bruchgleichungen beachten?
A: Die Regeln der Mathematik müsst ihr natürlich beachten, welche ihr unter den Rechenregeln findet. Wer noch Probleme bei Gleichungen mit Klammern hat, kann dies gerne auch noch nachlesen.
F: Welches Thema soll ich als nächstes lernen?
Nach dem Thema Bruchgleichungen bieten sich natürlich noch die Ungleichungen und die Bruchungleichungen an.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
