Dezimalzahl umwandeln in Bruch
Geschrieben von: Dennis RudolphDonnerstag, 28. Dezember 2017 um 20:30 Uhr
Wie man eine Dezimalzahl (Kommazahl) in einen Bruch umwandelt, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, wie man Kommazahlen in Brüche umrechnet.
- Viele Beispiele zu den verschiedenen Fällen der Umwandlung.
- Aufgaben / Übungen damit ihr Dezimalzahl zu Bruch und umgekehrt umwandeln lernt.
- Ein Video zu Dezimalzahlen.
- Ein Frage- und Antwortbereich zu diesem Bereich.
Hinweis: Wer sich für das Umwandeln von Dezimalzahlen in Brüche interessiert, der weiß normalerweise bereits, was ein Bruch und was eine Dezimalzahl ist. Falls nicht, bitte zunächst in Dezimalzahlen (Kommazahlen) Definition und Bruchrechnen reinsehen.
Erklärung Dezimalzahl in Bruch
Wie kann man eine Zahl (Dezimalzahl) in einen Bruch umwandeln? Leider muss man hier drei Fälle unterscheiden:
- Endliche Dezimalzahl
- Reinperiodische Dezimalzahl
- Gemischtperiodische Dezimalzahl
Fangen wir mit dem einfachsten Fall an: Der endlichen Dezimalzahl, also der endlichen Kommazahl.
Endliche Dezimalzahl (Kommazahl) in Bruch umwandeln:
In den meisten Fällen hat man eine endliche Dezimalzahl zum Umwandeln. Beispiele für endliche Dezimalzahlen wären:
- 2,342
- 1,5439
- 6,7
- 0,078
Die Umwandlung ist hier ganz einfach:
- Im Zähler steht die Dezimalzahl ohne Komma.
- Im Nenner schreibt man eine 1.
- Hinter die 1 im Nenner so viele Nullen wie man Stellen hinter dem Komma der Dezimalzahl hat.
Machen wir dies doch gerade einmal für diese vier Zahlen.
Beispiel 1:
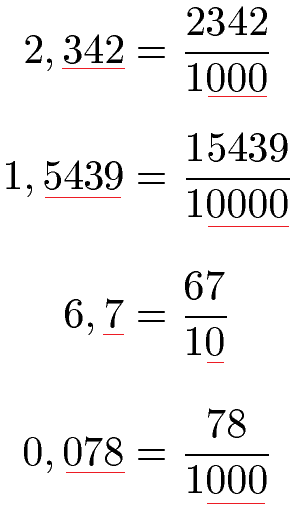
Hinweis: In manchen Fällen können Brüche noch gekürzt werden. Wie dies geht lernt ihr unter Brüche kürzen.
Anzeige:
Anzeigen:
Beispiele periodische Dezimalzahlen
In diesem Abschnitt sehen wir uns noch die Vorgehensweisen für reinperiodische Dezimalzahlen und gemischtperiodische Dezimalzahlen an. Bei periodischen Zahlen wiederholt sich eine oder mehr Zahlen immer und immer wieder.
Reinperiodische Dezimalzahlen:
Was sind reinperiodische Dezimalzahlen? Nun, eine reinperiodische Dezimalzahl ist eine Dezimalzahl, bei denen die Periode direkt nach dem Komma beginnt. Diese drei Dezimalzahlen wären reinperiodisch:
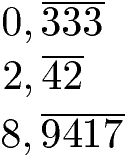
Vorgehensweise reinperiodische Dezimalzahlen in Bruch wandeln:
- Ganze Zahl vor dem Komma hinschreiben
- Pluszeichen schreiben
- Periodenangabe übernehmen in Zähler
- So viele 9er in Nenner wie Periode Stellen hat.
- Alles in einen Bruch umwandeln.
Beispiel 2a:
Zunächst soll 0,333... in einen Bruch umgewandelt werden. Wir haben vor dem Komma eine Null, diese übernehmen wir. Danach haben wir eine Periode mit 333, welche wir in den Zähler übernehmen. Dies sind auch 3 Stellen, daher schreiben wir drei Mal die 9 in den Nenner.
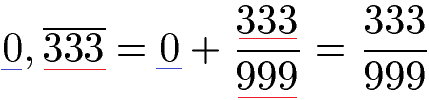
Die 0 vorne können wir auch wegfallen lassen. Es bleibt 333 : 999 übrig. Wir haben damit komplett in einen Bruch umgewandelt. Wer mag kann diesen Bruch kürzen.
Beispiel 2b:
Jetzt soll 2,424242... umgewandelt werden. Wir schreiben die 2 hin und ein Pluszeichen. Die Periode besteht aus 42, was wir in den Zähler schreiben. Dies sind auch 2 Stellen, daher schreiben wir in den Nenner zwei Mal die 9.
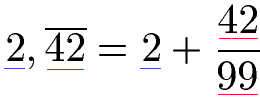
Wir können daraus noch einen Gesamtbruch machen. Dazu multiplizieren wir die 2 mit 99 und teilen durch 99. Dies ermöglicht uns die Zähler auszurechnen.
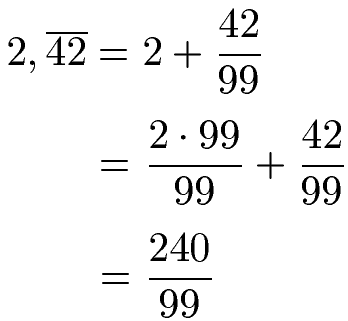
Beispiel 2c:
Noch ein Beispiel mit 8,9417... Wir spalten zunächst die 8 ab. Die vier Stellen hinter dem Komma (Periode) schreiben wir in den Zähler. Wegen 4 Stellen im Zähler schreiben wir vier 9er in den Nenner. Danach fassen wir zusammen, indem wir die 8 vorne mit 9999 : 9999 rechnen. Dadurch können wir im Zähler 8 · 9999 + 9417 = 89409 rechnen, im Nenner bleibt die 9999.
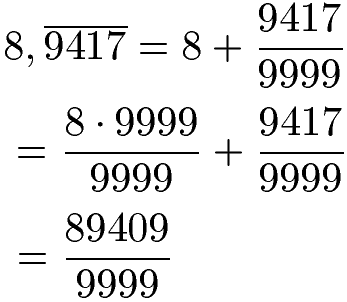
Gemischtperiodische Dezimalzahlen in Bruch wandeln:
Fehlen uns noch die gemischtperiodischen Zahlen, welche in einen Bruch umgewandelt werden sollen. Dies sind Dezimalzahlen, bei denen hinter dem Komma erst einmal eine oder mehrere Zahlen kommen und erst danach die Periode startet. Dies wären gemischtperiodische Dezimalzahlen:
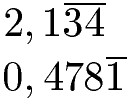
Vorgehensweise gemischtperiodische Dezimalzahlen in Bruch:
- Die Dezimalzahl solange mit 10 multiplizieren, bis hinter dem Komma nur noch der periodische Teil steht.
- Umwandeln wie eine ganzperiodische Zahl.
- Den ersten Schritt rückgängig machen.
Beispiel 3:
Es soll 2,1343434... in einen Bruch gewandelt werden. Wir haben eine Stelle hinter dem Komma, welche nicht zur Periode gehört. Da es nur eine Stelle ist, multiplizieren wir mit 10.
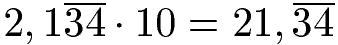
Wir trennen alles vor dem Komma ab. Danach ein Pluszeichen. Auf den Bruch dahinter schreiben wie in den Zähler 34. Die 34 hat zwei Stellen, daher zwei Mal die 9 in den Nenner.
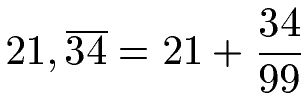
Wir fassen dies zusammen: Dazu multiplizieren wir die 21 mit 99 und teilen wieder durch 99. Was dies soll? Damit können wir ganz einfach im Zähler zusammenfassen: 21 · 99 + 34 = 2113 während die 99 im Nenner bleiben.
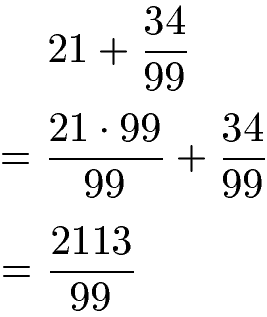
Wir haben am Anfang mit 10 multipliziert. Daher müssen wir jetzt noch durch 10 dividieren. Dies machen wir, indem wir im Nenner eine 0 anhängen. Wir erhalten:
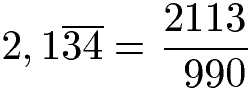
Beispiel 4:
Hier noch schnell die Rechnung für 0,478181... Wir haben dabei zwei Stellen hinter dem Komma, die nicht zur Periode gehören. Daher multiplizieren wir erst mit 100 und dividieren ganz am Ende wieder durch 100.
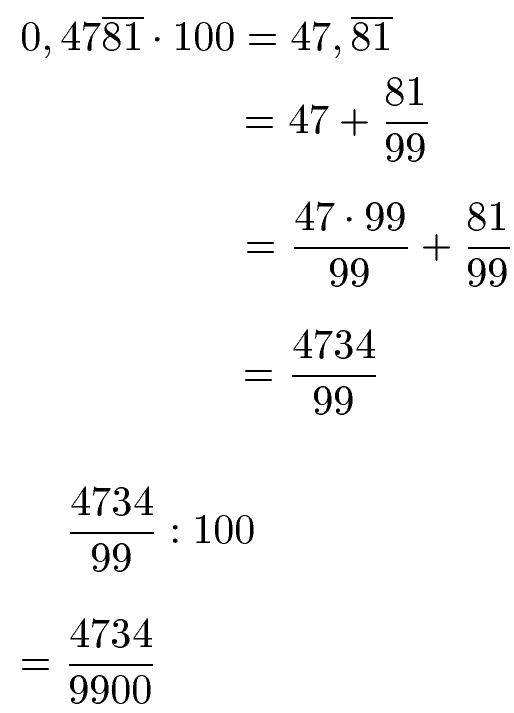
Aufgaben / Übungen Dezimalzahlen umwandeln
Anzeigen:Videos Dezimalzahlen
Rechnen mit Dezimalzahlen
Wir haben noch kein direktes Video zum Umrechnen von Dezimalzahlen in Brüche. Allerdings solltet ihr trotzdem das Rechnen mit Dezimalzahlen können. Dies sehen wir uns daher im Video an:
- Definition Dezimalzahlen
- Addition Kommazahlen
- Subtraktion Kommazahlen
- Multiplikation von Dezimalzahlen
- Division von Dezimalzahlen
Nächstes Video »
Fragen mit Antworten Zahl in Bruch
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zu Dezimalzahlen und Brüche an.
F: Wie funktioniert der umgekehrte Fall: Bruch in Dezimalzahl wandeln?
A: Ein Bruch ist nicht anderes als eine Division von Zahlen. Daher kann man auch den umgekehrten Weg gehen und einen Bruch in eine Dezimalzahl umwandeln. Wie dies geht lernt ihr unter Bruch in Dezimalzahl.
F: Wie funktioniert das Rechnen mit Dezimalzahlen?
A: Ihr solltet mit Dezimalzahlen (Kommazahlen) rechnen lernen. Dies sind die Grundrechenarten Addition, Subtraktion, Multiplikation und Division. Auch eine Mischung von diesen Grundrechenarten solltet ihr beherrschen. Viele Erklärungen und Beispiele dazu findet ihr unter Dezimalzahlen (Kommazahlen) rechnen.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
