ggT: Größter gemeinsamer Teiler
Geschrieben von: Dennis RudolphDienstag, 14. Dezember 2021 um 11:23 Uhr
Mit dem größten gemeinsamen Teiler - kurz ggT - befassen wir uns hier. Dies sehen wir uns an:
- Eine Erklärung, was das ggT ist und wie man es berechnet.
- Viele Beispiele zur ggT-Berechnung, auch mit Primfaktorzerlegung.
- Aufgaben / Übungen rund um den größten gemeinsamen Teiler.
- Ein Video zum Thema.
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Tipp: Falls ihr Verständnisprobleme mit diesem Artikel habt, dann klemmt es vielleicht bei den Vorkenntnissen. Falls dem so ist seht erst einmal auf die Inhalte Teilbarkeitsregeln und Primfaktorzerlegung.
Erklärung ggT
Was beim größten gemeinsamen Teiler gesucht wird, steckt eigentlich schon im Namen. Wir sehen uns die Teiler von zwei Zahlen (oder mehr) an und schauen dann, wo für beide Zahlen der Teiler am größten ist. Es gibt etliche Wege die Teiler zu berechnen. Einige davon sollen hier gezeigt werden.
Starten wir mit dem Berechnen des ggT für kleine Zahlen. Bei Zahlen bis in etwa 50 kann man die Teilbarkeitsregeln einsetzen um die Teiler der jeweiligen Zahlen zu ermitteln. Zur Erinnerung noch einmal die ersten Regeln zur Teilbarkeit. Alternativ kann man auch einfach die Zahl nehmen und diese durch 2, 3, 4, 5, etc. im Kopf teilen und sehen, ob die Berechnung ohne Rest möglich ist.
- Eine Zahl ist durch 2 teilbar wenn sie eine gerade Zahl ist.
- Eine Zahl ist durch 3 teilbar, wenn ihre Quersumme durch 3 teilbar ist.
- Eine Zahl ist durch 4 teilbar, wenn die letzten beiden Stellen der Zahl durch 4 teilbar sind.
- Eine Zahl ist durch 5 teilbar, wenn die letzte Stelle eine 0 oder 5 ist.
- Eine Zahl ist durch 6 teilbar, wenn diese durch 2 und durch 3 teilbar ist. Wir wenden damit die Teilungsregeln für 2 und 3 von oben an.
Beispiel 1:
Der größte gemeinsame Teiler - kurz ggT - der Zahlen 8 und 12 soll gefunden werden. Wie lautet dieser?
Lösung:
Wir müssen sowohl für die 8 als auch für die 12 alle Teiler aufschreiben. Wir teilen die 8 daher (im Kopf) durch 2, 3, 4 etc. und sehen, wo sich die Zahl jeweils ohne Rest teilen lässt. Dies tun wir auch für die 12. Die Teiler 1 und die Zahl selbst lassen wir dabei außen vor, da diese trivial sind. Die Teiler sind damit:
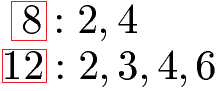
Wir suchen die größte gemeinsame Zahl aus beiden Zahlenreihen heraus. Dies ist die 4.
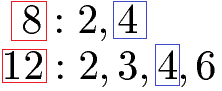
Der größte gemeinsame Teiler von 8 und 12 ist damit die 4.
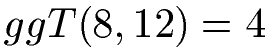
Beispiel 2:
Das ggT von drei Zahlen soll berechnet werden. Die Zahlen sind 12, 16 und 24. Wie lautet dieser?
Lösung:
Wir ermitteln zuerst für alle drei Zahlen die gemeinsamen Teiler. Dazu nehmen wir jede Zahl und teilen diese durch 2, 3, 4, 5 etc. Geht eine Division ohne Rest auf, nehmen wir diese in die Zahlenreihe auf. Die Teiler 1 und die Zahl selbst lassen wir dabei außen vor, da diese trivial sind. Die Teiler sind damit:

Die 4 ist der größte gemeinsame Teiler aller drei Zahlen.
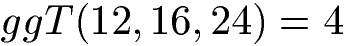
Es muss nicht immer einen größten gemeinsamen Teiler geben. Zwei natürliche Zahlen a und b sind dann teilerfremd, wenn es keine natürliche Zahl außer der Eins gibt, die beide Zahlen teilt.
Anzeige:
Anzeigen:
Beispiele ggT Primfaktorzerlegung
Werden die Zahlen etwas größer ermittelt man das ggT eher mit der Primfaktorzerlegung. Denn bei größeren Zahlen ist es schon sehr viel aufwändiger alle Teiler einzeln zu berechnen. Bei der Primfaktorzerlegung für den größten gemeinsamen Teiler nimmt man zunächst alle Ausgangszahlen und zerlegt diese in die Multiplikation kleiner Primzahlen. Man bezeichnet diese dann als Primfaktoren.
Beispiel 3:
Das ggT von 99 und 132 soll mit der Primfaktorzerlegung ermittelt werden. Wie lautet es?
Lösung:
Wir zerlegen zunächst beide Zahlen. Dazu prüfen wir zunächst bei jeder einzelnen Zerlegung, ob eine Zahl durch 2 teilbar ist. Falls nein, versuchen wir durch 3 zu teilen und so weiter. Wer das nächste Beispiel trotz gründlichem Ansehen nicht versteht, sieht bitte noch in die Primfaktorzerlegung rein. Zunächst die Zerlegung in Primfaktoren:
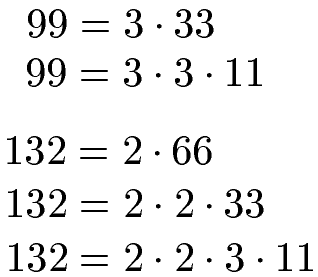
Wir haben nun die 99 und die 132 in eine Multiplikation kleiner Primzahlen zerlegt. Nun schreiben wir dies als Potenzen:
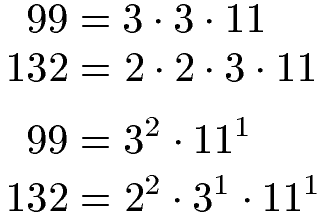
Um den ggT zu berechnen, nimmt man die Primfaktoren, die in beiden Primfaktorzerlegungen vorkommen und den jeweils kleinsten Exponenten haben. Dies sind dann 31 und bei 111 ist es natürlich egal (da beide den Exponenten 1 haben). Die 22 fliegt raus, da sie nur in einer der beiden Zerlegungen vorkommt.
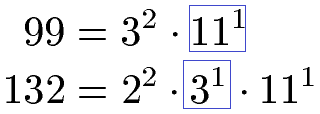
Diese multiplizieren wir miteinander und erhalten als ggT die Zahl 33.
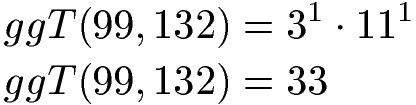
Aufgaben / Übungen ggT
Anzeigen:Videos ggT
Erklärungen ggT als Video
Im nächsten Video wird das ggT behandelt. Zum Inhalt?
- Wofür steht ggT?
- Was versteht man unter dem ggT?
- Wie berechnet man den größten gemeinsamen Teiler?
- Beispiele.
- Erklärungen.
Nächstes Video »
Fragen mit Antworten ggT
In diesem Abschnitt werden typische Fragen zum ggT behandelt.
F: Wie findet man das ggT bei sehr großen Zahlen?
A: Bei sehr großen Zahlen werden natürlich PCs, Taschenrechner oder andere elektronische Hilfsmittel eingesetzt. Diese setzen verschiedene Algorithmen ein, um das Ergebnis zu berechnen. Diese umfassen zum Beispiel den euklidischen Algorithmus oder den steinschen Algorithmus. Dennoch sollte das Thema für kleine Zahlen in der Schule behandelt werden (ab der 5. Klasse), damit Schüler und Schülerinnen ein Verständnis für diesen Bereich der Mathematik erlangen.
F: Welche Themen sollte ich als nächstes lernen?
A: Neben dem ggT gibt es auch noch das kgV, den kleinsten gemeinsamen Vielfachen. Ich empfehle außerdem noch einen Blick auf die wichtigsten Rechenregeln der Mathematik.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
