Krümmungsverhalten / Krümmung

Mit der Krümmung bzw. dem Krümmungsverhalten von Funktionen befassen wir uns hier. Dies sehen wir uns an:

• Eine Erklärung, was man unter der Krümmung von Funktionen versteht.
• Beispiele für die Berechnung des Krümmungsverhaltens.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu Wendepunkten.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Um das Krümmungsverhalten zu verstehen, ist es hilfreich, wenn ihr bereits Ableitungsregeln und Wendepunkte kennt.

Krümmung Erklärung

Beginnen wir ganz kurz mit einer Definition zum Krümmungsverhalten:

Merke:

• Die erste Ableitung einer Funktion gibt ihr Steigungsverhalten an.
• Die zweite Ableitung einer Funktion gibt ihr Krümmungsverhalten an.

Stellt euch vor, dass ihr mit einem Auto oder einem Fahrrad eine Kurve lang fahrt. Je nachdem, ob ihr das Lenkrad nach rechts einschlagen müsst oder nach links bezeichnet man diese Kurve oder Funktion als linksgekrümmt (konvex) oder rechtsgekrümmt (konkav).

Rechtskrümmung:

Bei der Rechtskrümmung ist die zweite Ableitung an der Stelle x kleiner Null: f''(x) < 0. Die Rechtskrümmung wird auch als konkav bezeichnet. Die nächste Grafik zeigt zwei rechtsgekrümmte Verläufe.

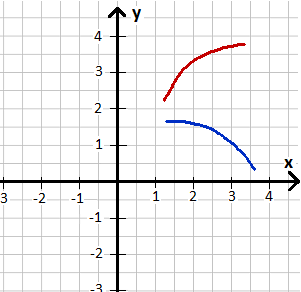
Linkskrümmung:

Bei der Linkskrümmung ist die zweite Ableitung an der Stelle x größer als Null: f''(x) > 0. Die Linkskrümmung wird auch als konvex bezeichnet. Die nächste Grafik zeigt zwei linksgekrümmte Verläufe.

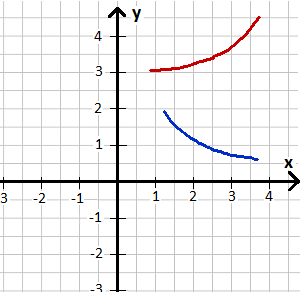
Anzeige:

Beispiel Krümmung

Sehen wir uns Beispiele zur Berechnung des Krümmungsverhaltens an.

Beispiel 1: Krümmung ermitteln

Ist die folgende Funktion konvex oder konkav?

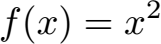
Lösung:

Wir leiten die Funktion zwei Mal ab. Die zweite Ableitung hat dabei kein x, also bleibt nur eine Zahl übrig. Da 2 größer als 0 ist haben wir eine konvexe Funktion, sprich die Funktion ist linksgekrümmt.

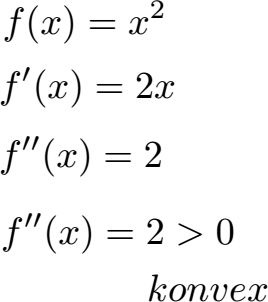
Beispiel 2: Krümmungsverhalten berechnen

Ermittelte das Krümmungsverhalten der folgenden Funktion.

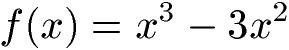
Lösung:

Mit der Potenzregel bilden wir die ersten drei Ableitungen.

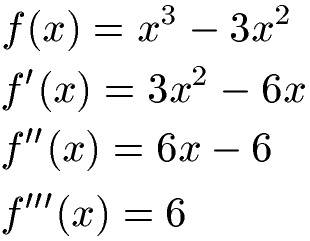
Wie man sehen kann kommt in der zweiten Ableitung ein x vor. Dies bedeutet, dass die Funktion verschiedene Krümmungsverhalten aufweisen kann. Daher suchen wir nach einem Wendepunkt in der Funktion. Hinweis: Der Wendepunkt ist der Punkt einer Funktion an dem sich das Krümmungsverhalten ändert.

Wer noch nichts über den Wendepunkt weiß sieht bitte in Wendepunkt / Wendestelle berechnen rein. Um diesen zu ermitteln setzen wie die zweite Ableitung gleich Null und erhalten einen möglichen Wendepunkt bei x = 1.

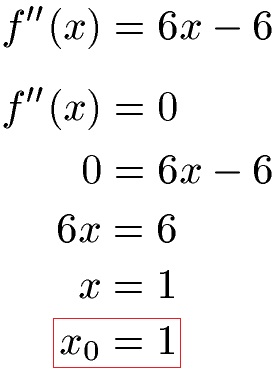
Um zu prüfen das wir wirklich einen Wendepunkt haben benötigen wir noch die dritte Ableitung. Diese ist an der Stelle x = 1 ungleich 0. Daher liegt bei x = 1 wirklich eine Wendestelle / Wendepunkt vor.

Um das Krümmungsverhalten der Funktion zu ermitteln sehen wir uns die Krümmung vor und nach dem Wendepunkt an. Da der Wendepunkt bei x = 1 liegt können wir zum Beispiel x = 0,5 nehmen um die Krümmung davor zu ermitteln und x = 1,5 um die Krümmung nach dem Wendepunkt zu ermitteln. Sowohl x = 0,5 als auch x = 1,5 setzen wir in die zweite Ableitung ein. Ist dies kleiner 0 haben wir eine Rechtskrümmung (konkav). Bei größer 0 liegt eine Linkskrümmung (konvex) vor.

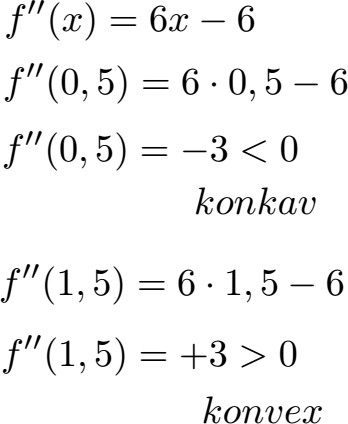
Betrachtet man die Funktion von links nach rechts geht die Funktion von einer Rechtskrümmung (konkav) in eine Linkskrümmung (konvex) über.

Aufgaben / Übungen Krümmung

Aufgabe 1:

Bevor wir rechnen zunächst ein paar Fragen.

• Welche Bedingung muss für eine Linkskrümmung erfüllt sein?

• f''(x) > 0
• f''(x) < 0
• f''(x) = 0
• f''(x) <= 0

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Wendepunkt

Fragen mit Antworten Krümmungsverhalten