Wendepunkt / Wendestelle berechnen

Was Wendestelle und Wendepunkt sind und wie man sie berechnet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was Wendepunkte und Wendestellen sind.
• Beispiele wie man diese Punkte berechnet.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu Wendepunkten.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Für die Berechnung von Wendepunkten ist es hilfreich, wenn ihr bereits Ableitungsregeln kennt und auch wisst was ein Extrempunkt ist.

Wendepunkt / Wendestelle Erklärung

Stellt euch vor ihr fahrt mit dem Fahrrad oder mit dem Auto durch eine Strecke mit vielen Kurven. Dabei bewegt ihr das Lenkrad hin und her, also von links nach rechts und wieder zurück. Der Wendepunkt ist die Stelle an dem das Lenkrad gerade steht (also da wo der Übergang von links nach rechts oder umgekehrt ist).

Dieser Punkt oder diese Stelle gibt es auch in der Mathematik. Definition Wendepunkt / Wendestelle:

Die nächste Grafik zeigt einen Wendepunkt:

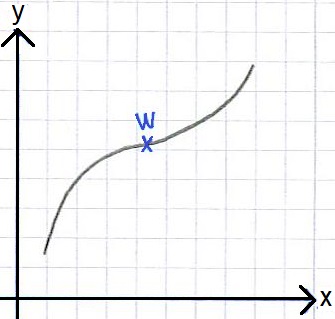
Den Wendepunkt findet man mit diesen Bedingungen:

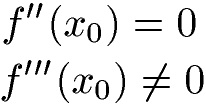
Anzeige:

Beispiel Wendepunkt / Wendestelle berechnen

In diesem Abschnitt soll ein Beispiel zu Wendestelle und Wendepunkt ausführlich besprochen und vorgerechnet werden. Da Schüler und Schülerinnen an unterschiedlichen Stellen scheitern geschieht dies Stück für Stück geschehen.

Beispiel 1: Wendepunkt / Wendestelle bestimmen

Wir haben die folgende Funktion:

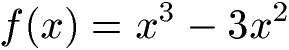
1a) Wo liegt die Wendestelle dieser Funktion?

1b) Wo liegt der Wendepunkt dieser Funktion?

1c) Wie groß ist die Steigung im Wendepunkt?

Lösung:

Wir benötigen zunächst die ersten drei Ableitungen der Funktion. Diese erhalten wir mit der Potenzregel.

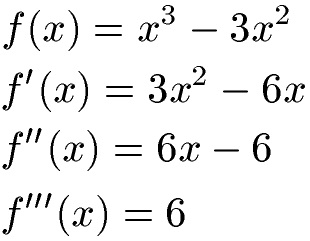
Um nun eine Wendestelle zu finden, setzen wir die zweite Ableitung gleich Null und berechnen x. Dabei nennen wir dieses x im Anschluss x₀, da dies unser Kandidat für eine Wendestelle ist.

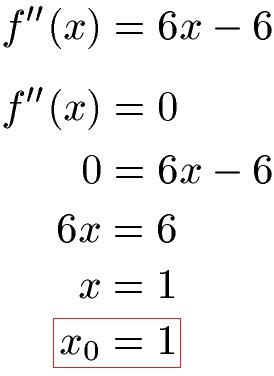
In die dritte Ableitung müssen wir theoretisch x = 1 einsetzen (wie eben berechnet). Da es jedoch kein x gibt haben wir einfach 6 in der dritten Ableitung und dies ist ungleich Null. Daher liegt bei x₀ = 1 ein Wendepunkt bzw. eine Wendestelle vor.

Wir wissen damit, dass bei x = 1 wirklich eine Wendestelle vorliegt. Um den Wendepunkt an dieser Stelle vollständig angeben zu können müssen wir noch f(x) berechnen.

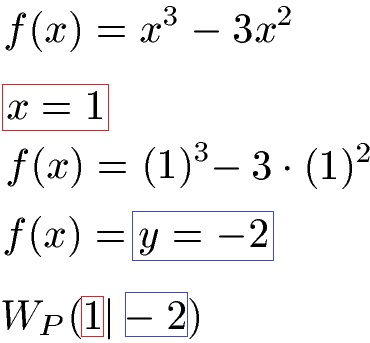
Wir wissen, dass die Wendestelle x = 1 ist und der Wendepunkt mit x = 1 und y = -2 angegeben werden kann: Fehlt uns noch die Steigung in genau diesem Punkt. Die erste Ableitung einer Funktion gibt die Steigung der Funktion an. Wir suchen die Steigung an der Stelle x = 1 ein. Daher setzen wir in die erste Ableitung x = 1 ein und erhalten eine Steigung von -3.

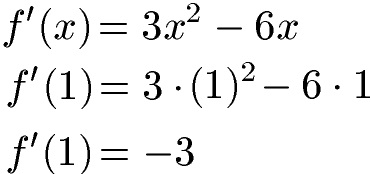
Aufgaben / Übungen Wendepunkte

Aufgabe 1:

Wo liegt bei der nächsten Funktion der Wendepunkt?

• x = 2; y = 2/3
• x = 3; y = 2
• x = 4; y = -10
• x = -2; y = -4

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Wendepunkt

Fragen mit Antworten zum Wendepunkt