Lineare Gleichungen lösen
Geschrieben von: Dennis RudolphSamstag, 23. November 2019 um 22:11 Uhr
Was lineare Gleichungen sind und wie man sie löst, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung wie man lineare Gleichungen löst
- Beispiele für das Lösen von linearen Gleichungen.
- Aufgaben / Übungen damit ihr dies selbst üben könnt.
- Ein Video zum Lösen von Gleichungen.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Wir sehen uns hier an wie man lineare Gleichungen löst. Wem dies nicht langt, der kann sich gerne noch ansehen wie man einfache Gleichungen löst. Dies findet ihr unter Gleichungen auflösen / umstellen.
Erklärung lineare Gleichungen lösen
Was sind lineare Gleichungen? Sehen wir uns dazu eine Definition an:
Eine lineare Gleichung (mit einer Variablen) ist eine Gleichung in der folgenden Form oder kann auf diese Form gebracht werden:
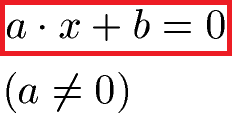
Dies nächsten drei Gleichungen sind linear, denn sie haben die Form von weiter oben oder können auf diese Form gebracht werden:
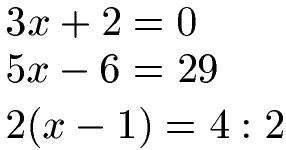
Eine lineare Gleichung wird gelöst, indem man nach der Variablen auflöst. In diesem Fall ist die Variable x. Am Ende soll die Gleichung so aussehen, das wir x = .... dastehen haben. Sehen wir uns dabei einige Beispiele an.
Vorgehensweise:
- Gleichungen löst man, indem man auf beiden Seiten der Gleichung die selben Rechenschritte durchführt.
- Addiere ich auf der linken Seite die Zahl 5, muss ich dies auch auf der rechten Seite der Gleichung machen.
- Dabei führt man die Rechenschritte so durch, dass am Ende die Variable x auf einer Seite stehen bleibt und alles andere auf der anderen Seite.
Anzeige:
Anzeigen:
Beispiel lineare Gleichungen lösen
Sehen wir uns einige Beispiele zum Lösen von linearen Gleichungen an.
Beispiel 1:
Löse die Gleichung 4x - 8 = 0.
Lösung:
Um diese Gleichung nach x aufzulösen, addieren wir zunächst +8 auf beiden Seiten der Gleichung. Dadurch fällt die -8 links weg und rechts erhalten wir 0 + 8 = 8. Die jeweiligen Rechenschritte kann man hinter einen Strich schreiben. Um nach x aufzulösen müssen wird die 4x noch durch 4 teilen. Dadurch erhalten wir links 1x und rechts 8 : 4 = 2. Die Lösung der Gleichung lautet x = 2.
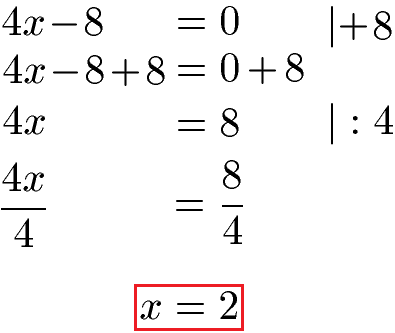
Beispiel 2:
Die Gleichung 2(x - 1) = 8 + 4 : 2 soll berechnet werden. Wie groß ist x?
Lösung:
Auf der linken Seite der Gleichung lösen wir zunächst die Klammer auf. Dazu nehmen wir die 2 vor der Klammer und multiplizieren diese mit x. Dadurch erhalten wir 2x. Außerdem nehmen wir die 2 vor der Klammer und multiplizieren diese noch mit der -1 in der Klammer. Dies ergibt -2. Auf der rechten Seite müssen wir Punkt vor Strich beachten, daher führen wir zunächst die Division 4 : 2 = 2 aus. Um nach x aufzulösen, müssen wir die -2 auf der linken Seite beseitigen. Dafür müssen wir +2 auf beiden Seiten rechnen. Wir erhalten dadurch 2x = 12. Wir teilen beide Seiten durch 2 und erhalten dadurch x = 6.
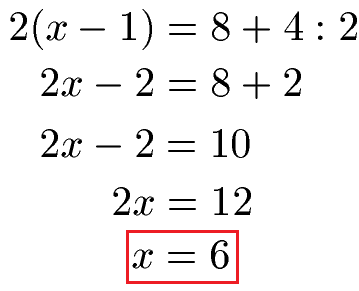
Weitere Beispiele zum Lösen einfacher Gleichungen findet ihr unter Gleichung auflösen / umstellen.
Aufgaben / Übungen lineare Gleichungen
Anzeigen:Video Gleichung lösen
Einfache Gleichungen lösen
Im nächsten Video lernt ihr wie man einfache Gleichungen lösen kann:
- Dabei wird erklärt, was eine Gleichung überhaupt ist und wie man diese löst.
- Entsprechende Beispiele werden dazu vorgerechnet.
Nächstes Video »
Fragen mit Antworten lineare Gleichungen
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zu linearen Gleichungen an.
F: Welche Arten von linearen Gleichungen gibt es noch?
A: Weiter oben wurden lineare Gleichungen mit einer Variablen behandelt. Es gibt jedoch auch noch lineare Gleichungen mit zwei Variablen. In der Schule haben diese Gleichungen in den meisten Fällen nicht nur die Variable x, sondern die Variablen x und y.
F: Welche Themen sollte ich mir als nächstes ansehen?
A: Neben dem Lösen von linearen Gleichungen - auch mit zwei Variablen - gibt es lineare Gleichungssysteme. Dabei handelt es sich um mehrere Gleichungen, die zusammenhängen und gemeinsam gelöst werden müssen. Gleichungen können auch nichtlinear sein. Bei einer Potenz zweiten Grades nennt man dies quadratische Gleichung, bei einer Potenz dritten Grades kubische Gleichung. Neben Gleichungen gibt es außerdem Ungleichungen. Diese Inhalte sind bereits verfügbar:
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
