Rechteck Umfang

Wie man den Umfang von einem Rechteck berechnet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung mit Formel zum Umfang von einem Rechteck.
• Viele Beispiele mit Zahlen und Einheiten und ein beliebter Fehler.
• Aufgaben / Übungen damit ihr alles selbst üben könnt.
• Ein Video zu diesem Thema.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Hinweis: Beim Berechnen vom Umfang eines Rechtecks tauchen gleich Variablen (Buchstaben) auf. Eine Variable ist ein Platzhalter für eine Zahl. Wer dazu erst noch mehr lesen möchte, kann gerne noch in Was ist eine Variable? rein sehen. Ein Rechteck hat eine Länge und eine Breite. Diese Angaben setzt man in Meter, Zentimeter oder einer anderen Längeneinheit ein. Wer davon noch nie etwas gehört hat, kann gerne erst noch in die Längeneinheiten rein sehen.

Erklärung Umfang Rechteck

Was ist ein Rechteck? Nun ein Rechteck hat vier Ecken und vier rechte Winkel. Die nächste Grafik zeigt euch, wie ein Rechteck aussieht.

Stellt euch vor dieses Rechteck wäre ein Grundstück mit einem Haus darauf. Dann könnte man sich die Fragen stellen, wie viele Meter man laufen muss, um einmal um das Grundstück runderum zu kommen. Genau dies ist der Umfang. Um so etwas berechnen zu können, muss man wissen, wie Lange die Seiten des Rechtecks sind. Dabei sollte jedem Auffallen, dass die Seite links so lange ist wie die Seite rechts. Auch die Seiten oben und unten sind gleichlang.

Die nächste Grafik zeigt erneut das Rechteck, jedoch diesmal mit Variablen. Die eine Länge in grün mit der Variablen a und die andere Länge in rot mit der Variablen b. Es spielt für den Umfang von einem Rechteck keine Rolle, welche Länge als a und welche als b bezeichnet wird.

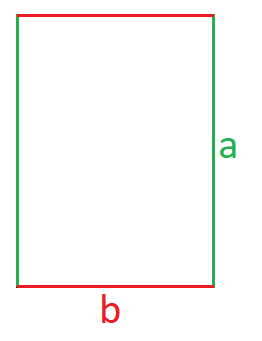
Wir können den Umfang berechnen, indem wir a + b + a + b berechnen. Wir müssen damit alle Seiten zusammenrechnen. Dies kann man zusammenfassen zu 2a + 2b. In der Formel wird für den Umfang ein großes U eingesetzt.

Formel Rechteck Umfang:

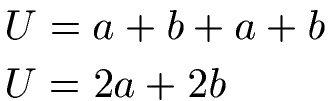
Manchmal kennt man den Umfang und möchte die Länge einer Seite berechnen. Dazu muss man die Formel zum Umfang vom Rechteck umstellen. Wie man dies selbst macht, seht ihr weiter unten. Das Ergebnis der Umstellung soll hier aber bereits kurz gezeigt werden.

Formel Rechteck Umfang umgestellt:

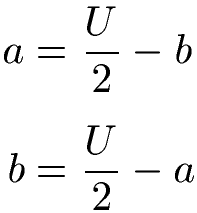
Anzeige:

Beispiele Umfang Rechteck

In diesem Abschnitt sollen viele Beispiele mit Zahlen und Einheiten vorgerechnet werden.

Beispiel 1:

Die Seiten eines Rechtecks seien 7 cm und 9 cm lang. Wie groß ist der Umfang?

Lösung:

Wir setzen a = 7 cm und b = 9 cm ein und berechnen damit den Umfang mit der Formel weiter oben zu 32 cm.

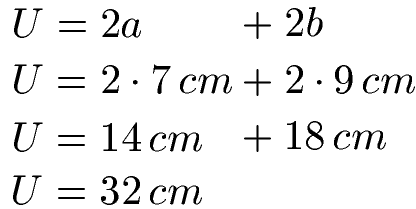
Beispiel 2:

Der Umfang von einem Rechteck sei 30 cm. Außerdem kennen wir die Seitenlänge b mit 10 cm. Wie lang ist a?

Lösung:

Wir setzen in die nach a umgestellte Formel von oben ein und rechnen damit a aus.

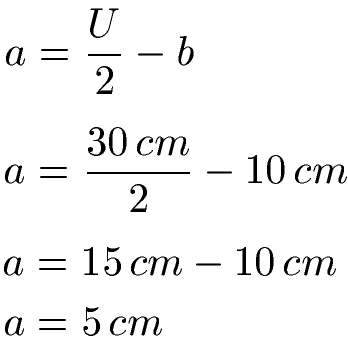
Beispiel 3:

Zum Umfang von einem Rechteck noch eine Textaufgabe: "Ein Grundstück sei 30 Meter lang und 2000 Zentimeter breit. Das Grundstück hat die Form eines Rechtecks". Ein Schüler hat die Aufgabe den Umfang zu berechnen und dem Lehrer diese Lösung hingelegt. Was hat er falsch gemacht? Wie lautet der richtige Umfang?

Lösung:

Der Schüler hat mit Meter und Zentimeter zwei verschiedene Einheiten verwendet. Dies darf man nicht. Bei der Berechnung müssen gleiche Einheiten verwendet werden. Daher rechnen wir die 2000 Zentimeter zu 20 Meter um und rechnen erneut. Das Mischen von Einheiten ist ein typischer Fehler. Außerdem hat er vor dem b die 2 vergessen. Auch dies müssen wir bei der Neuberechnung richtig machen.

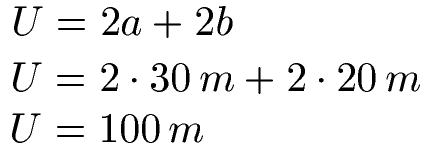
Beispiel 4:

Im letzten Beispiel soll das Umstellen der Formel noch einmal ausführlich gemacht werden. Die Formel U = 2a + 2b soll nach a und b jeweils umgestellt werden. Wie macht man dies?

Lösung:

Um nach a umzustellen, subtrahieren wir zunächst 2b auf beiden Seiten der Gleichung. Um von 2a auf a zu kommen müssen wir noch durch 2 teilen. Dies bedeutet, dass wir U durch 2 teilen sowie -2b durch 2 (dabei kürzt sich die 2) und 2a : 2 = a. Die Vorgehensweise um nach b aufzulösen sieht auch so aus.

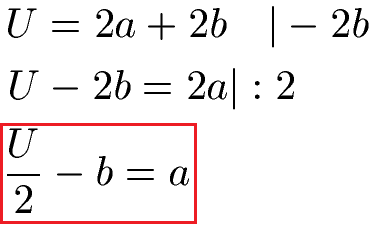
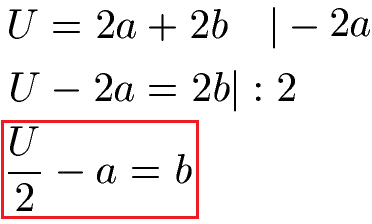
Rechteck Übungsaufgaben

Aufgabe 1: Bevor wir rechnen eine kurze Frage zum Aufwärmen. Mit welcher Formel berechnet man die Fläche von einem Rechteck?

• A = a * b
• U = 2a + 2b
• U = a + b
• A = 2a * b

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Rechteck Umfang

Hinweise zu den Übungsaufgaben