Spatprodukt berechnen mit Formel

Wie man das Spatprodukt berechnet und wozu man dies braucht, lernt ihr hier. Dies sind die Themen:

• Eine Erklärung, was das Spatprodukt ist.
• Beispiele wie man das Spatprodukt von 3 Vektoren berechnet.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zum Spatprodukt.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es tauchen bei der Berechnung vom Spatprodukt die Begriffe Vektorprodukt (Kreuzprodukt), Skalarprodukt und Determinante auf. Diese Themen werden hier noch einmal in Kürze wiederholt. Falls euch dies nicht reicht solltet ihr jedoch noch einmal die genannten Themen nachlesen.

Spatprodukt Eigenschaften und Berechnung

Wozu braucht man das Spatprodukt?

Die nächste Grafik zeigt wie drei Vektoren ein Volumen aufspannen können.

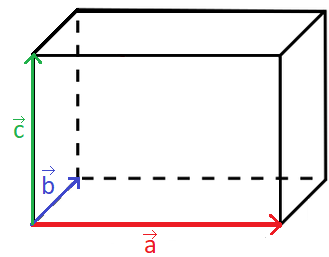
Dieses Volumen kann man auf verschiedene Art und Weise berechnet werden. Wir starten mit dem Kreuzprodukt und Skalarprodukt und rechnen weiter unten genau dieses Beispiel noch einmal mit einer Determinante aus.

Beispiel 1: Spatprodukt mit Kreuzprodukt und Skalarprodukt

Wir haben die drei folgenden Vektoren. Berechne das Volumen.

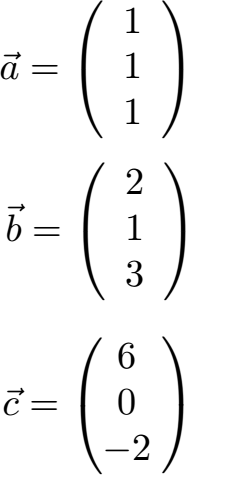
Lösung:

Die allgemeine Formel für das Vektorprodukt (Kreuzprodukt) ist diese:

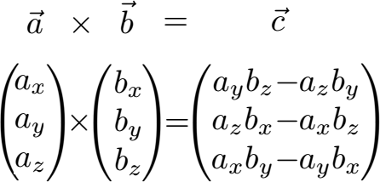
Daher nehmen wir uns zwei der Vektoren und setzen einfach die entsprechenden Zahlen in die Formel ein:

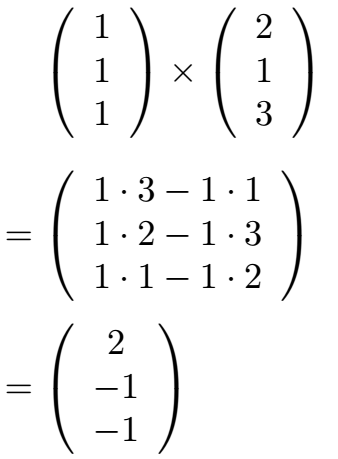
Mit 2, -1 und -1 erhalten wir einen neuen Vektor. Wir nehmen den dritten Ausgangsvektor mit hinzu und setzen einen dicken Malpunkt (für das Skalarprodukt) dazwischen. Dieses berechnen wird nun Zeile für Zeile.

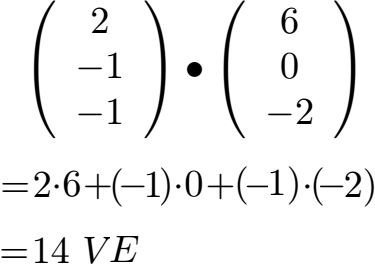
Als Ergebnis erhalten wir 14. Da keine Einheiten wie Zentimeter, Meter etc. gegeben waren schreiben wir stattdessen Volumeneinheiten, kurz VE dahinter. Die drei Vektoren spannen damit ein Volumen von 14 VE auf.

Anzeige:

Spatprodukt mit Determinante

Es gibt eine weitere Möglichkeit das Volumen zu berechnen. Wir nehmen dazu erneut unsere drei Vektoren:

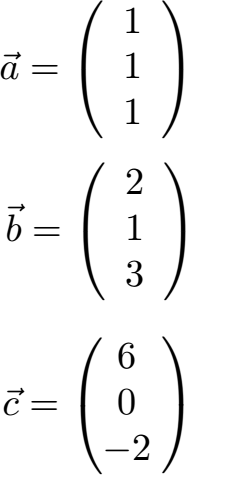
Diese drei Vektoren schreiben wir jetzt in eine Determinante:

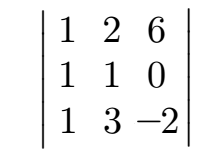
Die allgemeine Berechnung der Determinante erfolgt nach diesem Zusammenhang.

Setzen wir die Zahlen ein erhalten wir das Volumen wie folgt:

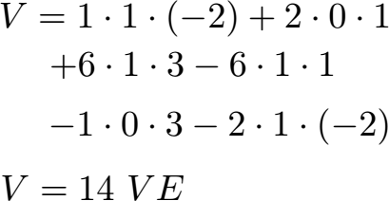
Auch bei der Berechnung über die Determinante erhalten wir das Volumen zu 14, besser gesagt 14 Volumeneinheiten (VE).

Aufgaben / Übungen Spatprodukt

Aufgabe 1:

In diesem Bereich erhaltet ihr die Möglichkeit das Spatprodukt zu üben. Da einige Schüler und Studenten jedoch bereits an einfachen Fragen scheitern, gibt es bei uns auch Fragen zum Thema.

• Was berechnet man mit dem Spatprodukt?

• Volumen
• Länge
• Fläche
• Winkel

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Spatprodukt

Fragen mit Antworten zum Spatprodukt