Zahlenreihen fortsetzen / vervollständigen

Wie man Zahlenreihen fortsetzen bzw. vervollständigen kann wird in diesem Artikel behandelt. Dies sehen wir uns an:

• Eine Erklärung, was Zahlenreihen sind und wie man diese fortsetzt bzw. vervollständigt.
• Viele Beispiele werden vorgerechnet.
• Aufgaben / Übungen damit ihr selbst lernt eine Reihe zu vervollständigen.
• Ein Video zu Zahlenreihen mit entsprechenden Beispielen.
• Ein Frage- und Antwortbereich mit typischen Fragen zu diesem Thema.

Um Zahlenreihen vervollständigen zu können, solltet ihr die Grundrechenarten kennen. Dabei geht es darum einfache Zahlen zu addieren oder subtrahieren, zu multiplizieren und zu dividieren. Wer davon noch gar keine Ahnung hat, soll dies bitte erst einmal nachlesen.

Erklärung: Zahlenreihen lernen

Wie funktioniert das mit den Zahlenreihen? Starten wir mit einer Erklärung zu diesem Thema.

Kommen wir zu einigen Zahlenreihen und welche Regeln hinter diesen stehen. Schaut euch an, welche Regeln hier typisch sind. Denn solche Regeln sollen bei den den späteren Beispielen und den Aufgaben gefunden und angewendet werden.

Zahlreihe Nr. 1:

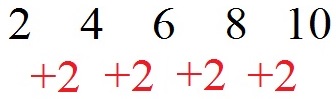
• Die erste Zahlenreihe ist ganz einfach. Wir haben 2, 4, 6, 8 und 10.
• Hier ist es einfach zu erkennen, dass wir jedes Mal +2 rechnen müssen.

Zahlenreihe Nr. 2:

• Diese Reihe aus Zeilen besteht aus 1, 3, 9, 27, 81
• Man kann dies erreichen, wenn man die vorige Zahl jeweils mit 3 multipliziert.

Zahlenreihe Nr. 3:

• Gegeben sei die Zahlenreihe 2, 8, 4, 16 und 8.
• Hier müssen wir etwas gründlich hinsehen.
  • Zunächst einmal müssen wir von 2 auf 8 kommen. Dies können wir mit +6 oder mit ·4 erreichen.
• Im Anschluss von 8 auf 4.
  • Dies schaffen wir mit -4 oder mit :2.
• Danach müssen wir von 4 auf 16 kommen.
  • Dies erreichen wir mit ·4 oder mit + 12.
  • Da wir die Regel ·4 auch vorne hatten, übernehmen wir diese
• Im Anschluss müssen wir von 16 auf 8 kommen.
  • Dies erreichen wir mit -8 oder mit :2.
  • Das :2 hatten wir vorne bereits, daher nehmen wir die Regel :2.

Anzeige:

Beispiele für Zahlenreihen

In diesem Abschnitt sollen noch eine Reihe an weiteren Beispielen vorgerechnet werden. Dabei werden erst einmal die Aufgaben so gezeigt, wie diese auch in der Schule gestellt werden. Diese muss man sich genau ansehen, um die richtige Regeln zu finden.

Beispiel 1:

Gegeben sei die folgende Zahlenreihe. Welche Zahl muss ergänzt werden?

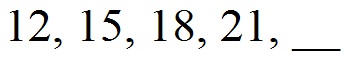
Lösung:

Schaut man sich die Reihe an, dann sieht man, dass jeweils +3 gerechnet wird. Daher rechnen wir diese auf die 21 drauf. 21 + 3 = 24.

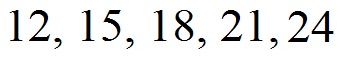
Beispiel 2:

Eine weitere Zahlenreihe sei gegeben. Welche Zahl fehlt am Ende?

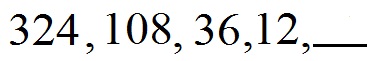
Lösung:

Hier wurde jeweils durch 3 geteilt. Daher 12 : 3 = 4 am Ende.

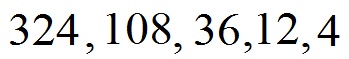
Aufgaben / Übungen Zahlenreihen

Aufgabe 1:

• Mit welcher Zahl muss diese Reihe fortgesetzt werden? 3, 6, 9, 12...

• 14
• 15
• 10
• 16

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Reihe von Zahlen Video

Fragen mit Antworten Zahlenreihen