Ebene: Koordinatengleichung in Normalenform

Die Umwandlung einer Ebene von einer Koordinatengleichung in die Normalenform sehen wir uns hier an. Dies sind die Themen:

• Eine Erklärung, wie man Ebenen umwandelt.
• Beispiele für die Umwandlung von Koordinatendarstellung in die Normalenform.
• Aufgaben / Übungen zum Umwandeln von Ebenen.
• Ein Video zur Ebenenumwandlung.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich, wenn ihr bereits wisst, wie man Gleichungen umformt. Falls nicht könnt ihr euch dies gerne noch ansehen. Ansonsten gehen wir hier an die Ebenenumwandlung von einer Koordinatengleichung in die Normalenform.

Koordinatengleichung in Normalenform Erklärung

Von der Koordinatenform auf die Normalenform kommt man in dem man indem man den Normalenvektor abliest und einen Ortsvektor findet.

Beispiel 1:

Wie lautet diese Koordinatengleichung in Normalenform?

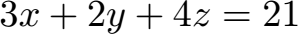
Lösung:

Den Normalenvektor n können wir direkt aus der Gleichung ablesen. Fehlt uns noch der Ortsvektor. Diesen erhalten wir indem wir y = 0 und z = 0 in der Koordinatengleichung setzen. Wir können dadurch x = 7 berechnen. Damit haben wir alles was wir für die Normalenform wissen müssen: Wir setzen den Ortsvektor mit x = 7, y = 0 und z = 0 ein sowie den Normalenvektor.

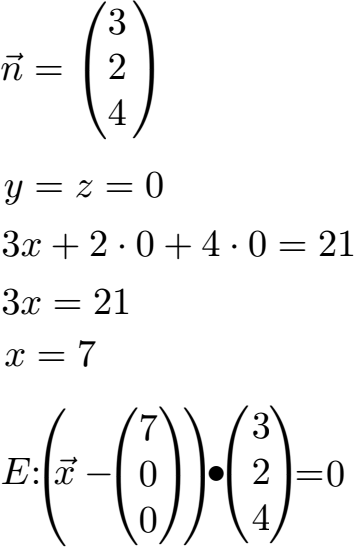
Anzeige:

Koordinatengleichung in Normalenform Beispiel 2

Sehen wir uns ein weiteres Beispiel zur Umwandlung von Koordinatenform in Normalenform an.

Beispiel 2:

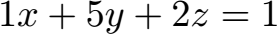
Lösung:

Wir lesen den Normalenvektor mit 1, 5 und 2 ganz einfach aus der Gleichung ab. Um den Ortsvektor zu finden setzen wir y = 0 und z = 0. Tun wir dies in der Koordinatengleichung erhalten wir x = 1. Ortsvektor und Normalenvektor sind gefunden und müssen einfach nur in die Schreibweise der Normalenform eingetragen werden.

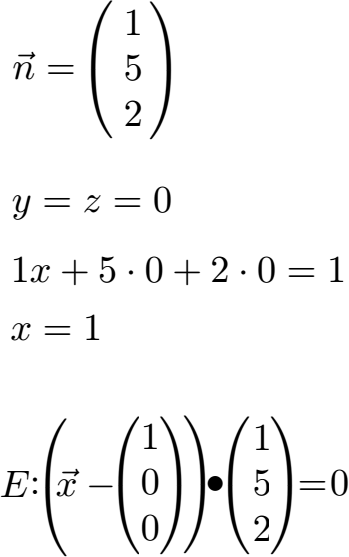
Aufgaben / Übungen Ebenengleichungen umwandeln

Aufgabe 1:

In diesem Bereich erhaltet ihr die Möglichkeit die Ebenengleichungen umzuwandeln.

• Wandele mit einem linearen Gleichungssystem die folgende Parametergleichung in eine Koordinatengleichung um. Wie lautet die Lösung?

• 2x + 3y - z = 10,5
• 5x + 1,5y - z = 8
• 3x + 1,5y + 3z = 10,5
• 5x + 1,5y - z = 10,5

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Ebene umformen Video

Fragen mit Antworten: Koordinatengleichung in Normalenform