Ebene: Parametergleichung in Normalenform

Die Umwandlung einer Ebene von einer Parametergleichung in Normalenform sehen wir uns hier an. Dies sind die Themen:

• Eine Erklärung, wie man Ebenen umwandelt.
• Beispiele für die Umwandlung von Parameterdarstellung in Normalenform.
• Aufgaben / Übungen zum Umwandeln von Ebenen.
• Ein Video zur Ebenenumwandlung.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Um diese Ebenenumwandlung durchzuführen braucht ihr das Kreuzprodukt. Dieses behandeln wir hier auch gleich noch. Falls ihr noch mehr darüber wissen wollt oder nicht alles versteht werft zusätzlich noch einen Blick in Kreuzprodukt / Vektorprodukt.

Parametergleichung in Normalenform Erklärung

In der analytischen Geometrie geht es manchmal darum eine Gleichung einer Ebenen umzuformen. Hier sehen wir uns an wie man von einer Ebenengleichung in Parameterform in eine Ebenengleichung in Normalenform kommt. Sehen wir uns die Vorgehensweise an.

Vorgehensweise:

1. Wir nehmen die beiden Richtungsvektoren der Ebene und bilden einen Normalvektor. Dazu benötigen wir das Kreuzprodukt. Wie man dieses ausrechnet zeigt die nächste Grafik.

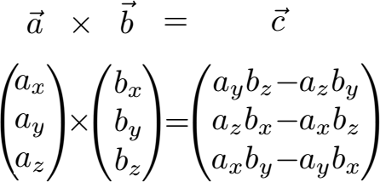
2. Danach brauchen wir nur noch den Ortsvektor von der Parameterform. Dies ist nichts anderes als der Punkt vorne in der Ebenengleichung.

3. Mit dem Normalenvektor vom Kreuzprodukt und dem Punkt der Ebenengleichung bilden wir die Ebene in Normalenform.

Anzeige:

Parametergleichung in Normalenform Beispiel

Sehen wir uns ein Beispiel an.

Beispiel 1: Ebene umwandeln

Wandle diese Parametergleichung in Normalenform um.

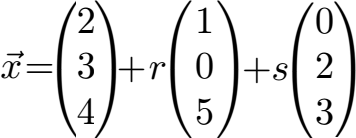
Lösung:

Wir bilden das Kreuzprodukt mit der oben angegeben Gleichung und rechnen den Normalenvektor n aus. Danach nehmen wir uns noch den Punkt (2;3;4). Mit beidem bilden wir die Ebene in Normalenform.

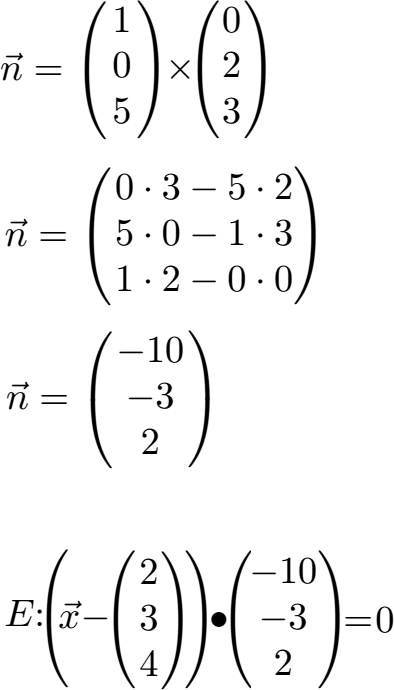
Aufgaben / Übungen Ebenengleichungen umwandeln

Aufgabe 1:

In diesem Bereich erhaltet ihr die Möglichkeit die Ebenengleichungen umzuwandeln.

• Wandele mit einem linearen Gleichungssystem die folgende Parametergleichung in eine Koordinatengleichung um. Wie lautet die Lösung?

• 3x + 1,5y + 3z = 10,5
• 5x + 1,5y - z = 8
• 5x + 1,5y - z = 10,5
• 2x + 3y - z = 10,5

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Ebene umwandeln

Fragen mit Antworten: Ebene Parameterform in Normalenform