Halbschriftlich Rechnen

Mit dem halbschriftlichen Rechnen befassen wir uns in diesem Artikel. Die Inhalte in Kurzform:

• Eine Erklärung, was halbschriftliches Rechnen ist und welche Formen es gibt.
• Beispiele zum halbschriftlichen Rechnen mit Zahlen.
• Aufgaben / Übungen zu den verschiedenen Formen des halbschriftlichen Rechnens.
• Videos zum schriftlichen Rechnen.
• Ein Frage- und Antwortbereich mit typischen Fragen zu diesem Thema.

Dieser Artikel ist eine kurze Zusammenfassung zum halbschriftlichen Rechnen. Wer ausführlich die verschiedenen Varianten kennenlernen möchte, der findet hier noch eine Liste mit den ausführlichen Artikeln:

• Halbschriftlich Addieren
• Halbschriftlich Subtrahieren
• Halbschriftlich Multiplizieren
• Halbschriftlich Dividieren

Erklärung halbschriftlich Rechnen

Was bedeutet halbschriftlich Rechnen? Also was heißt denn halbschriftlich Rechnen? Nun, darunter versteht man in der Mathematik ein Verfahren um mit etwas größeren Zahlen zu rechnen.

Grundsätzlich gilt: Zu den Verfahren Addieren, Subtrahieren, Multiplizieren und Dividieren gibt es oft verschiedene Wege diese durchzuführen. Wir stellen auf unserem Angebot jeweils eine ganz typische Vorgehensweise dazu vor, sonst führen die verschiedenen Verfahren zur Verwirrung.

Vorteile halbschriftliches Rechnen:

• Eine große Rechenaufgabe kann in mehrere kleine Aufgaben zerlegt werden.
• Die Aufgaben können ohne Taschenrechner gelöst werden.
• Das halbschriftliche Rechnen verbessert das Verständnis der Mathematik.

Nachteile halbschriftliches Rechnen:

• Es sind mehrere Rechenschritte nötig, bei denen man auch Fehler machen kann.
• Es ist einiges an Schreibarbeit nötig, um die Teilaufgaben zu lösen.
• Wer nur das halbschriftliche Teilen lernt und nicht das schriftliche Teilen, dem fehlen oft Grundlagen für die Polynomdivision.

Soweit dazu, warum man das halbschriftliche Rechnen durchführt. Als nächstes sehen wir uns Beispiele zum halbschriftlichen Rechnen an.

Anzeige:

Beispiele halbschriftliches Rechnen

Sehen wir uns zu jeder Rechenart noch jeweils ein Beispiel an.

Beispiel 1:

Starten wir beim halbschriftlichen Rechnen mit der Addition. Berechnet werden soll 21 + 34. Um dies zu erreichen, unterteilen wir die Aufgabe in zwei kleinere Aufgaben. Dabei addieren wir die Einerstelle und die Zehnerstelle. Dies ergibt 50 und 5. Und diese beiden Addieren wir noch: 50 + 5 = 55. Damit erhalten wir die Lösung der Gesamtaufgabe: 21 + 34 = 55.

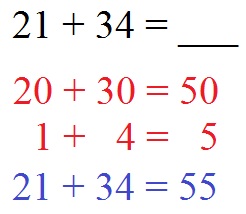
Weitere Beispiele im Artikel halbschriftliche Addition.

Beispiel 2:

Das nächste Beispiel zeigt die halbschriftliche Subtraktion. Berechnet werden soll 55 - 39. Dazu ziehen wir zunächst die Zehnerstelle ab, danach wird von diesem Ergebnis noch die Einerstelle abgezogen. Bleiben 16 am Ende übrig.

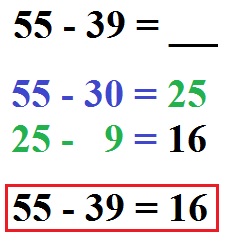
Weitere Beispiele im Artikel halbschriftliche Subtraktion.

Beispiel 3:

Kommen wir zum halbschriftlichen Multiplizieren. Berechnet werden soll 7 · 16. Dazu unterteilen wir diese Aufgabe in zwei Teilaufgaben, bei denen wir mit der Zehnerstelle und der Einerstelle multiplizieren. Am Ende werden die beiden Teilergebnisse addiert.

Weitere Beispiele im Artikel halbschriftliche Multiplikation.

Beispiel 4:

Fehlt noch das halbschriftliche Dividieren. Die halbschriftliche Division führt man durch, indem man den Dividenden in Vielfache des Teilers zerlegt. Also zerlegen wir die vordere Zahl. Man sollte dabei versuchen, möglichst einfache Zahlen zu nehmen. Zum Beispiel mit 300 : 6 = 50 haben wir einen einfachen Start. Bleiben noch 84 übrig, denn 384 - 300 = 84. Diese 84 zerlegen wir nun ebenfalls. Mit 60 : 6 = 10 haben erneut eine einfache Division. Ermitteln wir gerade noch was übrig bleibt: 384 - 300 - 60 = 24. Also bleibt 24 : 6 = 4. Die Teilergebnisse müssen noch addiert werden. 50 +10 + 4 = 64. Damit ergibt sich 384 : 6 = 64.

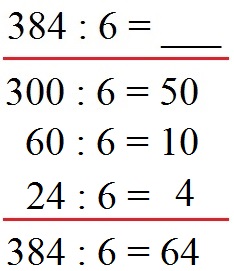
Noch mehr Beispiele im Artikel halbschriftliche Division.

Aufgaben / Übungen halbschriftlich Rechnen

Ihr solltet das halbschriftliche Rechnen auch selbst üben. Denn nur wer Aufgaben selbst rechnet, der wird fit in einem Thema. Wir haben die Übungen nach den vier Rechentypen unterteilt:

• Halbschriftlich Addieren Aufgaben / Übungen
• Halbschriftlich Subtrahieren Aufgaben / Übungen
• Halbschriftlich Multiplizieren Aufgaben / Übungen
• Halbschriftlich Dividieren Aufgaben / Übungen

Für alle Übungen liegen Musterlösungen vor. Versucht die Aufgaben jedoch erst einmal selbst zu bearbeiten, bevor ihr euch die Lösung anzeigen lasst.

Anzeigen:

Halbschriftlich Rechnen Videos

Fehlen uns noch Videos zum Rechen mit größeren Zahlen. Hier noch die entsprechenden Links:

• Video (halb)schriftlich Addieren
• Video (halb)schriftlich Subtrahieren
• Video (halb)schriftlich Multiplizieren
• Video (halb)schriftlich Dividieren

In unseren Sektionen bieten wir allgemein Videos zu größeren Zahlen an. Dabei sehen wir uns auch schriftliche Addition, schriftliche Subtraktion, schriftliche Multiplikation und schriftliche Division / Teilen an.

Fragen und Antworten zum halbschriftlichen Rechnen