Schnittpunkt zweier Geraden
Geschrieben von: Dennis RudolphDienstag, 23. Juni 2020 um 12:16 Uhr
Den Schnittpunkt zweier Geraden sehen wir uns hier an. Dies sind die Themen:
- Eine Erklärung, wie man den Schnittpunkt zweier Geraden findet.
- Beispiel für die Berechnung von einem Schnittpunkt.
- Aufgaben / Übungen um dieses Thema zu üben.
- Ein Video zum Schnittpunkt zweier Geraden.
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Tipp: Es ist hilfreich, wenn ihr bereits wisst, wie man Gleichungen umformt. Falls nicht könnt ihr euch dies gerne noch ansehen. Ansonsten gehen wir hier an den Schnittpunkt von zwei Geraden ran.
Schnittpunkt zweier Geraden Erklärung
Um den Schnittpunkt zweier Geraden zu berechnen geht man so vor:
- Prüfen, ob die Richtungsvektoren parallel sind.
- Falls nein: Gleichungssystem aufstellen.
- Gleichungssystem berechnen und falls lösbar .
- Schnittpunkt berechnen.
Beispiel 1: Schnittpunkt zweier Geraden
Finde heraus, ob sich die Geraden g und h schneiden und wenn ja in welchem Punkt?
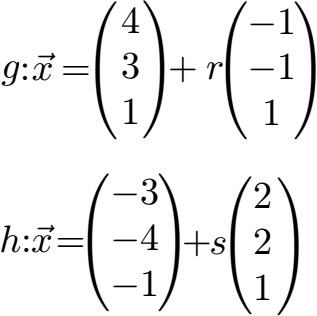
Lösung:
Wir prüfen zunächst ob die beiden Richtungsvektoren der Geraden parallel sind. Falls dem so ist sind die Geraden parallel und wir brauchen gar nicht nach einem Schnittpunkt zu suchen. Um dies zu tun bilden wir Zeile für Zeile bei den Richtungsvektoren Gleichungen und berechnen k.
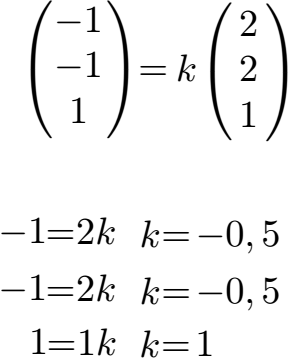
Wie man sehen kann sind die k verschieden. Aus diesem Grund sind die Geraden nicht parallel und wir können versuchen einen Schnittpunkt zu finden.
Anzeige:
Anzeigen:
Schnittpunkt zweier Geraden Beispiel
Um jetzt einen möglichen Schnittpunkt zu berechnen, nehmen wir uns noch einmal die Geraden:
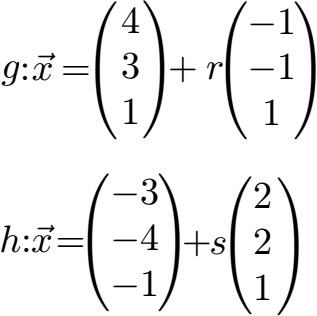
Wir bilden mit den Geraden drei Gleichungen, die Zeile für Zeile erstellt werden. Die erste Gleichung stellen wir nach r um.
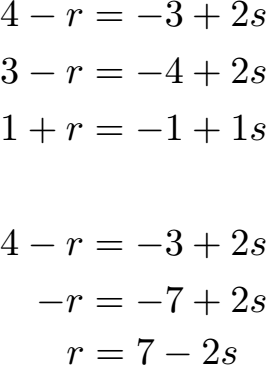
Mit r = 7 - 2s gehen wir in die unterste der drei Gleichungen und berechnen s = 3. Mit s gehen wir in eine der anderen Gleichungen in denen noch r vorhanden ist und berechnen r = 1.
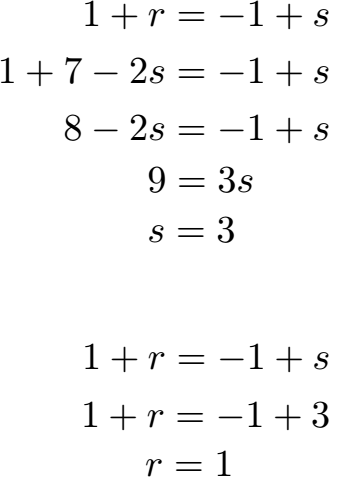
Setzen wir entweder r oder s ein bei einer der beiden Geradengleichungen können wir den Schnittpunkt berechnen. Dieser liegt bei x = 3, y = 2 und z = 2.
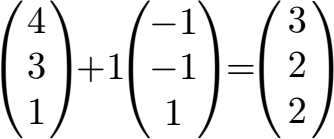
Aufgaben / Übungen Schnittpunkt Geraden
Anzeigen:Video Schnittpunkt zweier Geraden
Erklärung und Beispiele
Wie findet man den Schnittpunkt von 2 Graden? Das nächste Video zeigt eine grafische und eine rechnerische Lösung für dieses Problem. Zunächst werden beide Funktionen in ein Koordinatensystem eingetragen, um den Schnittpunkt ablesen zu können. Allerdings stellen die Funktionen auch ein Gleichungssystem dar. Wir haben also Gleichungen mit Unbekannten. Mehr dazu im Video. Dieses Video habe ich auf Youtube.com gefunden.
Nächstes Video »
Fragen mit Antworten: Schnittpunkt zweier Geraden
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zum Schnittpunkt zweier Geraden an.
F: Ich verstehe das Thema nicht. Wie kann ich es lernen?
A: Wenn ihr das Thema Lagebeziehungen von Geraden nicht versteht solltet ihr erst einmal diese Themen lernen:
F: Wann wird dieses Thema in der Schule behandelt?
A: Der Schnittpunkt zweier Geraden wird in der Oberstufe behandelt, meistens ab der 11. Klasse.
F: Welche Themen sollte ich mir als nächstes ansehen?
A: Wir arbeiten aktuell an diesen Themen und werden sie nach der Veröffentlichung hier verlinken:
- Unterschied Ortsvektor und Richtungsvektor
- Betrag / Länge eines Vektors
- Rechnen mit Vektoren
- Vektoren addieren
- Vektoren subtrahieren
- Mittelpunkt einer Strecke
- Vektorprodukt / Kreuzprodukt
- Spatprodukt
- Abstand Punkt zu Gerade
- Abstand paralleler Geraden
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
