Schriftlich dividieren mit Rest

Das schriftliche Dividieren mit Rest sehen wir uns hier an. Dies haben wir für euch:

• Eine Erklärung, wie das schriftliche Dividieren mit Rest funktioniert.
• Einige Beispiele, die ausführlich vorgerechnet werden.
• Aufgaben / Übungen damit ihr das Thema selbst ein bisschen üben könnt.
• Ein Video zum schriftlichen Dividieren.
• Ein Frage- und Antwortbereich rund um das schriftliche Dividieren mit Rest.

Die schriftliche Division ist der schwierigste Bereich der schriftlichen Rechenverfahren. Wir sehen uns hier Stück für Stück das Thema an. Wer dennoch Probleme hat, sollte vielleicht noch einmal in den Artikel Division von Zahlen reinsehen. Alternativ kann man solche Aufgaben auch mit der halbschriftlichen Division rechnen.

Erklärung schriftlich Dividieren mit Rest

Sehen wir uns einmal Erklärungen zum schriftlichen Dividieren mit Rest an. Als Einleitung soll dazu 581 : 4 berechnet werden. Angenommen wir hätten 581 Äpfel und möchten diese auf 4 Personen verteilen. Wie viele Äpfel bekommt jeder? Kurz zu den Begriffen bei der Berechnung. Die Zahl vorne ist der Dividend, die zweite Zahl ist der Divisor und das Ergebnis ist der Quotient.

Wie löst man so etwas nun? Erst einmal schreiben wir die Aufgabe ohne Begriffe hin:

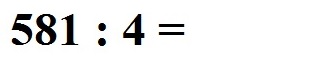
Wie oft passt die 4 in die 5 rein? Dies geht 1 mal. Diese 1 schreiben wir als erste Zahl in das Ergebnis (Quotient).

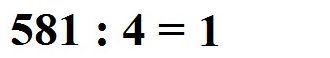
Danach müssen wir eine Multiplikation ausführen: 1 · 4 = 4. Diese 4 schreiben wir unter die 5.

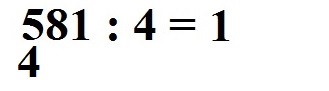
Jetzt müssen wir subtrahieren. Von der 5 ziehen wir die 4 ab. Dazu schreiben wir ein Minus-Zeichen vor die 4 und ein Strich darunter. 5 - 4 = 1.

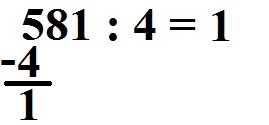
Wir ziehen die nächst Zahl runter. Dies ist die 8.

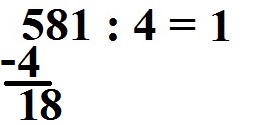
Nächste Frage: Wie oft passt die 4 in die 18? Sie geht 4 mal komplett rein, da 4 · 4 = 16 ergibt (und 4 · 5 = 20 ist zu groß). Die 4 geht in die 18 also 4 mal komplett rein. Daher schreiben wir die 4 ins Ergebnis.

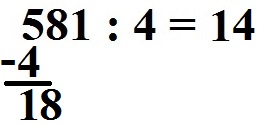
Wir rechnen wieder zurück mit 4 · 4 = 16 und schreiben dies unter die 18.

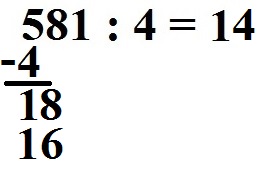
Wir können nun wieder subtrahieren: 18 - 16 = 2. Sieht dann so aus:

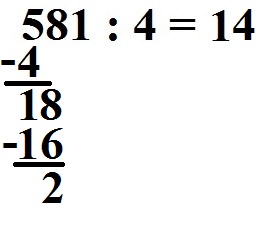
Fehlt uns noch die letzte Stelle: Dies ist die 1 und auch diese 1 ziehen wir runter.

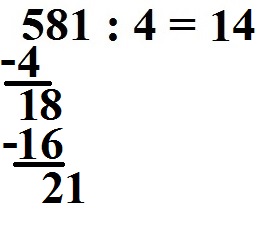
Wie oft geht nun die 4 in die 21? Dies geht 5 mal. Wir schreiben damit noch eine 5 in das Ergebnis.

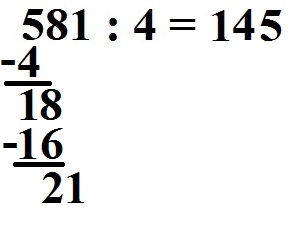
Multiplizieren wir wieder in die andere Richtung: 5 · 4 = 20.

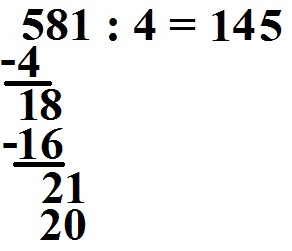
Wir subtrahieren wieder: 21 - 20 = 1. Die 1 ist unser Rest, also das was übrig bleibt.

Hätten wir 581 Äpfel und würden diese auf 4 Personen verteilen, dann würde jeder Person 145 Äpfel bekommen. Ein einziger Apfel würde übrig bleiben, dieser ist damit unser Rest. Natürlich könnte man diesen noch zerschneiden und ebenfalls verteilen.

Haben wir uns auch nicht verrechnet? Dies kann man mit einer Probe herausfinden:

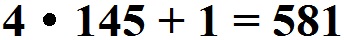
Anzeige:

Beispiele schriftlich Dividieren mit Rest

In diesem Abschnitt sehen wir uns weitere Beispiele zum schriftlichen Dividieren mit Rest an.

Beispiel 1:

Berechne mit der schriftlichen Division 313 : 6.

Lösung:

Hier zunächst die Rechnung, im Anschluss wird dieser erklärt.

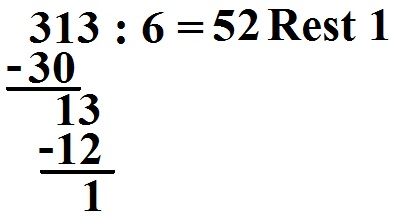
Wie kommt man darauf:

• Die 3 der ersten Zahl ist kleiner als die 6 durch welche geteilt werden soll.
• Daher nehmen wir noch die zweite Zahl mit dazu.
• Wir rechnen damit zunächst 31 : 6. In die 31 geht die 6 insgesamt 5 mal rein.
• Wir schreiben die 5 ins Ergebnis.
• Wir multiplizieren zurück: 5 · 6 = 30.
• Wir subtrahieren: 31 - 30 = 1.
• Wir ziehen die nächste Stelle runter. Dies ist eine 3.
• Wir erhalten damit die 13.
• Wir rechnen: 13 : 6. In die 13 geht die 6 insgesamt 2 mal rein.
• Die 2 schreiben wir in das Ergebnis.
• Wir multiplizieren zurück: 2 · 6 = 12.
• Und subtrahieren erneut: 13 - 12 = 1.
• Es gibt keine weitere Stelle mehr. Die 1 ist damit unser Rest.

Die Probe wäre 6 · 52 + 1 = 313

Beispiel 2:

Jetzt soll der Divisor mal etwas größer gewählt werden. Wir haben eine 50 durch die geteilt werden soll. Die Aufgabe lautet insgesamt 1283 : 50.

Lösung:

Zunächst die Lösung und danach die Erklärung.

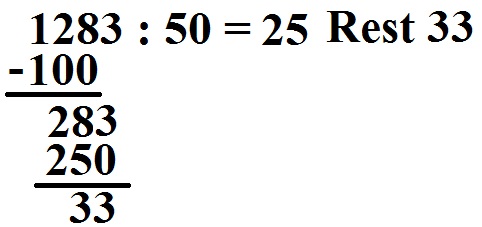
So wurde dies berechnet:

• Die 1 ist kleiner als die 50. Daher nehmen wir die nächste Stelle - eine 2 - mit dazu.
• Die 12 ist auch kleiner als die 50. Daher nehmen wir noch die 3. Stelle hinzu.
• 128 is größer als 50, daher fangen wir jetzt an zu rechnen.
• In die 128 geht die 50 insgesamt 2 mal rein. Wir schreiben die 2 ins Ergebnis.
• Wir multiplizieren zurück: 2 · 50 = 100.
• Wir subtrahieren: 128 - 100 = 28.
• Die nächste Stelle runterziehen: 3.
• Wir erhalten damit 283.
• In die 283 geht die 50 insgesamt 5 mal komplett rein. Die 5 schreiben wir ins Ergebnis.
• Wir multiplizieren zurück: 5 · 50 = 250.
• Wir subtrahieren wieder: 283 - 250 = 33.
• Keine weitere Stelle mehr vorhanden. Die 33 sind damit unser Rest.

Probe: 50 · 25 + 33 = 1283

Übungsaufgaben schriftlich Dividieren

Aufgabe 1: Fangen wir ganz einfach an. Berechne 450 : 5 mit der schriftlichen Division.

• 90
• 100
• 80
• 105

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.

Anzeigen:

Schriftlich Dividieren Video

Fragen mit Antworten: schriftliche Division mit Rest