Schriftlich multiplizieren: Erklärung und Beispiele

Das schriftliche Multiplizieren wird in diesem Artikel behandelt. Dies bekommt ihr erklärt:

• Eine Erklärung, wie das schriftliche Multiplizieren funktioniert.
• Viele Beispiele zum schriftlichen Multiplizieren.
• Aufgaben / Übungen damit ihr das schriftliche Multiplizieren üben könnt.
• Ein Video zum Thema schriftliche Multiplikation.
• Ein Frage- und Antwortbereich zum schriftlichen Multiplizieren.

Wir sehen uns hier die schriftliche Multiplikation an. Es hilft beim Verstehen dieses Artikels bereits einfache Additionen und Subtraktionen drauf zu haben. In einem weiterführenden Artikel sehen wir uns das schriftliche Multiplizieren mit Komma an.

Erklärung schriftlich Multiplizieren

In diesem Abschnitt sehen wir uns an, wie das schriftliche Multiplizieren funktioniert.

Wie funktioniert das schriftlichen Multiplizieren? Zunächst einmal sollte man sich merken, dasss man die kleinere Zahl als zweite Zahl verwendet. Dies erleichtert in den meisten Fällen die Berechnung. Dies gilt insbesondere wenn die Zahl weniger Stellen aufweist.

Sehen wir uns die Berechnung für 2134 · 2 einmal an.

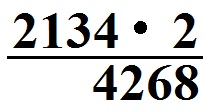
Wir haben hier mit der 2 eine einstellige Zahl. Die Einzelberechnung sieht so aus:

• 2 · 4 = 8
• 2 · 3 = 6
• 2 · 1 = 2
• 2 · 2 = 4
• Macht 4268 als Ergebnis.

Jetzt sehen wir uns das schriftliche Multiplizieren mit Übertrag an. Als Aufgabe dient 6718 · 4.

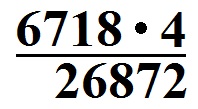
Die Berechnung macht man so:

• 4 · 8 = 32. Wir schreiben die 2 und haben die 3 als Übertrag.
• 4 · 1 = 4. Mit Übertrag kommen wir auf 4 + 3 = 7. Wir schreiben die 7.
• 4 · 7 = 28. Wir schreiben die 8 und haben die 2 als Übertrag.
• 4 · 6 = 24. Mit Übertrag kommen wir auf 24 + 2 = 26. Wir schreiben die 6 und haben die 2 als Übertrag.
• Keine Multiplikation mehr, wir schreiben daher einfach die 2.

Sehen wir uns noch ein schriftliches Multiplizieren mit einer zweistelligen Zahl an. Berechnet werden soll 3410 · 12.

Hier muss Schrittweise gerechnet werden:

• 3410 · 1 = 3410
• 3410 · 2 = 6820
• Die jeweils letzte Stelle - also die rote 0 und die grüne 0 - werden unter die rote 1 bzw. unter die grüne 2 geschrieben.
• Nun addieren wir Stelle für Stelle:
  • 0 = 0
  • 0 + 2 = 2
  • 1 + 8 = 9
  • 4 + 6 = 10. Wir schreiben 0 und haben einen Übertrag von 1.
  • 3 + 1 = 4

Anzeige:

Beispiele schriftlich Multiplizieren

In diesem Abschnitt sollen noch weitere Beispiele zum schriftlichen Multiplizieren behandelt werden.

Beispiel 1:

Hier missachten wir einmal den Tipp von oben und führen eine schriftliche Multiplikation so durch, dass die größere Zahl hinten steht. Dabei haben wir hier eine Multiplikation mit einer dreistelligen Zahl. Wie man sehen kann, geht dies auch, macht aber recht viel Arbeit. Berechnet werden soll 32 · 123.

Lösung:

Zunächst führen wir die Berechnungen durch:

• 1 · 32 = 32
• 2 · 32 = 64
• 3 · 32 = 96

Danach addieren wir:

• 6 = 6. Wir schreiben die 6.
• 4 + 9 = 13. Wir schreiben die 3 und übertragen 1 auf die nächste Stelle.
• 2 + 6 + 1 = 9. Wir schreiben die 9.
• 3 = 3. Wir schreiben die 3.

Beispiel 2:

Machen wir noch ein Beispiel für die schriftliche Multiplikation mit Komma. Berechnet werden soll 23 · 1,3.

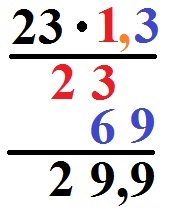
Wir rechnen zunächst so als gäbe es kein Komma:

• 1 · 23 = 23
• 3 · 23 = 69

Wir addieren die einzelnen Stellen:

• 9 = 9
• 3 + 6 = 9
• 2 = 2

Fehlen uns noch die Kommas:

• Bei der 23 haben wir kein Komma.
• Bei der 1,3 haben wir eine Stelle nach dem Komma.
• Die beiden Angaben addieren wir: 0 + 1 = 1.
• Wir müssen also das Komma im Ergebnis so setzen, dass es vor der letzten Stelle sitzt
• Aus 299 wird damit 29,9.

Noch nicht ganz klar? Wir haben einen Extra-Artikel dazu. Dieser findet sich unter schriftliche Multiplizieren mit Komma.

Übungsaufgaben schriftliche Multiplizieren

Aufgabe 1: Bevor ihr Aufgaben zum Rechnen bekommt eine ganz kurze Frage: Wozu dient die schriftliche Multiplikation normalerweise?

• Multiplikation großer Zahlen
• Faktoren berechnen
• Braucht man nie
• Ersetzt schriftliche Addition

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Schriftlich multiplizieren Video

Fragen mit Antworten zum schriftlichen Multiplizieren