Verknüpfungsgesetz / Verbindungsgesetz Mathe

Das Verbindungsgesetz - auch Verknüpfungsgesetz genannt - für Addition, Subtraktion und Brüche sehen wir uns hier an. Dies bekommt ihr:

• Eine Erklärung, was das Verbindungsgesetz besagt und welche Gleichungen es gibt.
• Viele Beispiele zur Anwendung des Verknüpfungsgesetzes.
• Aufgaben / Übungen damit ihr dieses Thema selbst üben könnt.
• Videos zu diesem Rechengesetz.
• Ein Frage- und Antwortbereich zu dieses Thema.

Wir sehen uns gleich das Verbindungsgesetz bzw. Verknüpfungsgesetz genauer an. Wer Probleme beim Verständnis bekommen sollte, dem helfen vielleicht noch die Artikel zu den Grundrechenarten: Dies sind Addition, Subtraktion, Multiplikation und Division. Ansonsten ran an das Assoziativgesetz.

Erklärung Verknüpfungsgesetz / Verbindungsgesetz

In der Fachsprache wird dieses Gesetz auch schlicht als Assoziativgesetz bezeichnet. Dieses gibt es für die Addition (plus rechnen) und für die Multiplikation (mal rechnen).

Verknüpfungsgesetz / Verbindungsgesetz der Addition:

Das Verknüpfungsgesetz der Addition besagt, dass es keine Rolle spielt, in welcher Reihenfolge man drei Zahlen addiert. Für die Addition sehen die Zusammenhänge so aus:

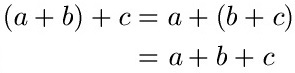
Für a, b und c setzen wir einmal irgendwelche Zahlen ein: Nehmen wir a = 2, b = 4 und c = 6.

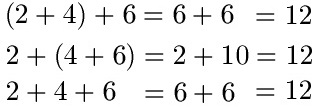
Egal welche der drei Berechnungswege wir verwenden, stets erhalten wir 12 als Ergebnis. Mehr Beispiele weiter unten.

Verknüpfungsgesetz / Verbindungsgesetz der Multiplikation:

Das Verknüpfungsgesetz der Multiplikation besagt, dass es egal ist, wie man drei Zahlen multipliziert. Für die Multiplikation sehen die Zusammenhänge so aus:

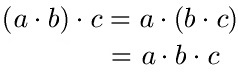
Auch hier setzen wir mal ein paar Zahlen ein. Nehmen wir für a = 2, b = 4 und c = 6 ein.

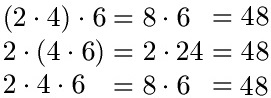
Auch hier kommen stets 48 als Produkt raus. Noch mehr vorgerechnete Aufgaben weiter unten.

Verknüpfungsgesetz / Verbindungsgesetz für Subtraktion, Division, Potenzen:

Das Verknüpfungsgesetz / Verbindungsgesetz gilt nicht für Subtraktion oder Division. Ebenso wenig für Potenzen.

Anzeige:

Beispiele Verknüpfungsgesetz / Verbindungsgesetz

In diesem Abschnitt sollen noch einige Beispiele zum Verbindungsgesetz vorgerechnet werden. Diese beinhalten Addition, Multiplikation und Brüche.

Beispiel 1:

Berechne 48 + 13 + 16 mit dem Verbindungsgesetz.

Lösung:

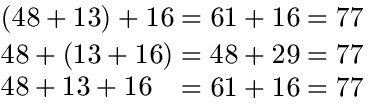
Beispiel 2:

Das Verbindungsgesetz soll für 4 · 2 · 3 verwendet werden.

Lösung:

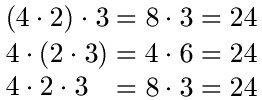
Beispiel 3:

Nun soll die Addition noch auf Brüche angewendet werden: 2/3 + 4/6 + 1/12.

Lösung:

Als Erstes müssen wir die Brüche auf einen gemeinsamen Nenner bringen. Dabei habe ich mir die 12 als gemeinsamen Nenner gewählt. Die Zähler müssen dann entsprechend angepasst werden und im Anschluss kann addiert werden.

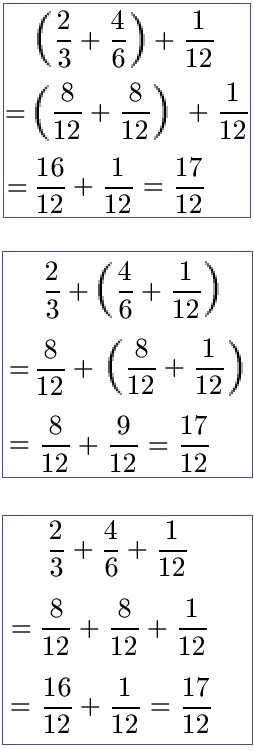
Aufgaben / Übungen Verbindungsgesetz

Aufgabe 1: Bevor wir rechnen ein paar kurze Fragen (wer diese nicht mag einfach auf "überspringen" klicken). Wo darf man das Assoziativgesetz denn überhaupt anwenden?

• Bei der Polynomdivision
• Subtraktion von drei Zahlen
• Division von drei Zahlen
• Addition von drei Zahlen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 9 Aufgaben erfolgreich gelöst.

Anzeigen:

Assoziativgesetz Video

Fragen mit Antworten Verknüpfungsgesetz