Verteilungsgesetz Mathematik
Geschrieben von: Dennis RudolphDonnerstag, 08. April 2021 um 16:44 Uhr
Das Verteilungsgesetz sehen wir uns hier an. Dies bekommt ihr:
- Eine Erklärung, was das Verteilungsgesetz besagt.
- Viele Beispiele zum Verteilungsgesetz.
- Aufgaben / Übungen zu diesem Gesetz.
- Videos zu diesem Thema.
- Ein Frage- und Antwortbereich zu diesem Rechengesetz.
Wir sehen uns gleich das Verteilungsgesetz an. Wer Schwierigkeiten beim Verständnis bekommen sollte, dem helfen vielleicht noch die Artikel zu den Grundrechenarten: Dies sind Addition, Subtraktion, Multiplikation und Division. Ansonsten ran an das dieses Rechengesetz.
Erklärung Verteilungsgesetz
Das Verteilungsgesetz ist ein Rechengesetz der Mathematik. In der Fachsprache wird dieses Gesetz oft auch Distributivgesetz genannt. Man verwendet dies dazu Klammern aufzulösen oder Klammern zu bilden. Zwei Gleichungen solltet ihr euch zunächst ansehen:
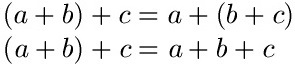
Die 1. Gleichung bezeichnet man als linksdistributiv und die 2.Gleichung als rechtsdistributiv. Zum besseren Verständnis setzen wir ein paar Zahlen ein.
Für die 1. Gleichung wird nun a = 2, b = 3 und c = 4 eingesetzt:
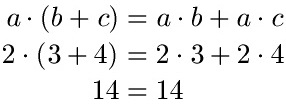
Jetzt noch für die 2. Gleichung. Auch hier a = 2, b = 3 und c = 4:
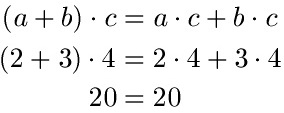
Es gibt noch eine Gleichung zum Verteilungsgesetz bei der Division:
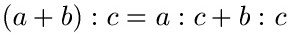
Auch hier setzen wir ein paar Zahlen ein. Nehmen wir a = 6, b = 8 und c = 10:
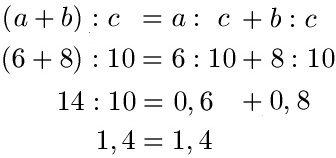
Im nächsten Abschnitt werden noch weitere Aufgaben vorgerechnet.
Anzeige:
Anzeigen:
Verteilungsgesetz Beispiele
Hier noch ein paar weitere Beispiele zu diesem Thema der Mathematik.
Beispiel 1:
Wende das Verteilungsgesetz auf 367 · 12 + 12 · 333 an.
Lösung:
Die 12 ist die gemeinsame Zahl bei beiden Multiplikationen. Daher können wir hier mit a · b + a · c = a · (b + c) loslegen. Und a = 12 ziehen wir vor die geöffnete Klammer.
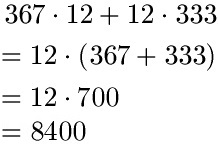
Beispiel 2:
Im nächsten Beispiel haben wir eine Teilung (Divisionsaufgabe). Die Aufgabe lautet (1100 - 33) : 11.
Lösung:
Wir nehmen die entsprechende Gleichung von oben für die Division. Wir ändern dies zunächst zu einer Schreibweise mit Brüchen und setzen im Anschluss die Zahlen ein. Danach rechnen wir die Brüche bzw. Subtraktion aus.
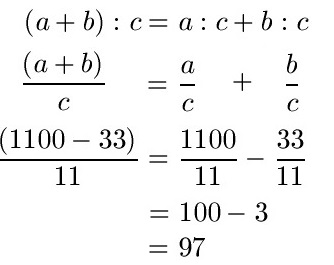
Beispiel 3:
Zeige, wie man von a · (b + c) auf a · b + a · c kommt.
Lösung:
Jedes Element in der Klammer wird mit dem Element vor der Kammer multipliziert. Siehe dazu die nächste Grafik.
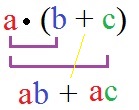
Aufgaben / Übungen Verteilungsgesetz
Anzeigen:Videos zum Verteilungsgesetz
Verteilungsgesetz Beispiele
Im nächsten Video wird das Verteilungsgesetz behandelt. Zunächst wird die Gleichung bzw. die Gleichungen hinter dem Gesetz vorgestellt und im Anschluss werden Übungen mit Zahlen vorgerechnet. Das Video ist für den Einstieg in dieses Thema geeignet.
Nächstes Video »
Verteilungsgesetz: Fragen mit Antworten
Hier noch ein paar typische Fragen mit Antworten zu diesem Gesetz..
F: Geht dies auch mit Brüchen?
A: Ja, auch bei Brüchen funktioniert dieses Gesetz. Hinter jedem Bruch steht eine Dezimalzahl. Zum Beispiel:
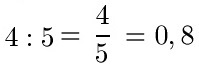
Für a, b und c kann man einen Bruch oder eine Dezimalzahl einsetzen.
F: Wozu braucht man dieses Gesetz eigentlich?
A: Das Verteilungsgesetz kann man verwenden um Klammern zu erstellen oder auszumultiplizieren. Ein Beispiel dafür sind die Binomischen Formeln. Wer sich dafür interessiert, bitte gleich weiter zu unserem Artikel Binomische Formeln.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
