Absolute und relative Häufigkeit

Was man unter absoluter und relativer Häufigkeit versteht, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was absolute und relative Häufigkeit sind.
• Beispiele für diese beiden Arten der Häufigkeit.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu den Grundlagen der Wahrscheinlichkeitsrechnung.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns gleich absolute und relative Häufigkeiten an. Viele Vorkenntnisse braucht ihr dazu nicht. Es hilft jedoch, wenn ihr bereits wisst, was ein Zufallsexperiment ist. Falls nicht erfahrt ihr dies unter Zufallsexperiment / Zufallsversuch.

Erklärung absolute Häufigkeit

Beginnen wir mit der absoluten Häufigkeit. Die Definition:

Beispiel 1: Absolute Häufigkeit

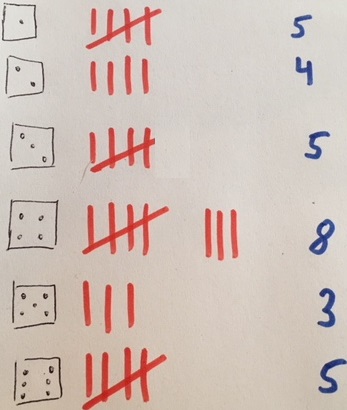
Wir nehmen einen normalen Würfel mit 6 Seiten. Wir würfeln diesen einige Male und führen eine Strichliste, wie oft welche Zahl fällt. Die Strichliste sieht danach so aus.

Wie hoch ist nun die absolute Häufigkeit der Zahlen? Wir zählen die Anzahl der Striche für die Würfelergebnisse 1 bis 6. Die absolute Häufigkeit gibt einfach an, wie oft welche Zahl gewürfelt wurde:

• Die absolute Häufigkeit der Zahl 1 ist 5.
• Die absolute Häufigkeit der Zahl 2 ist 4.
• Die absolute Häufigkeit der Zahl 3 ist 5.
• Die absolute Häufigkeit der Zahl 4 ist 8.
• Die absolute Häufigkeit der Zahl 5 ist 3.
• Die absolute Häufigkeit der Zahl 6 ist 5.

Die "Formel" welche hier oft gesucht wird gibt es hier in diesem Sinne nicht. Der Ausdruck H_n(x) ist damit so zu verstehen: Wir zählen die Anzahl der Würfe zusammen: 5 + 4 + 5 + 8 + 3 + 5 = 30. Damit haben wir n = 30. Dies ist unser kleines n nach H. In die Klammer kommt das Würfelergebnis, also 1 bis 6. Und hinter das Istgleich (=) wie oft ein Würfelergebnis gefallen ist.

• H₃₀(1) = 5
• H₃₀(2) = 4
• H₃₀(3) = 5
• H₃₀(4) = 8
• H₃₀(5) = 3
• H₃₀(6) = 5

Anzeige:

Beispiel relative Häufigkeit

Bei der absoluten Häufigkeit kam einfach raus, wie oft etwas passiert ist. Im Beispiel von oben wurde die Zahl 4 insgesamt 8 Mal gewürfelt. Aber ist das jetzt viel oder wenig? Um dies beurteilen zu können, gibt es noch die relative Häufigkeit. Damit gibt man den Anteil am Ganzen an. Beim Würfeln der Zahl 4 aus dem Beispiel wären dies 8 Würfe von 30 Würfe als relative Häufigkeit.

Sehen wir uns zunächst jedoch eine Definition für die relative Häufigkeit an:

Formel relative Häufigkeit:

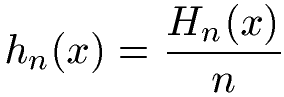
Beispiel 2: Relative Häufigkeit

Wir nehmen noch einmal den Würfelversuch von weiter oben und berechnen die relative Häufigkeit für die Augenzahlen 1 bis 6. Zunächst müssen wir wissen, wie oft insgesamt gewürfelt wurde. Dazu zählen wir alle Striche zusammen. Dies sind insgesamt 30. Die Anzahl ist damit 30, kurz n = 30. Die absoluten Häufigkeiten kennen wir auch schon, denn diese hatten wir oben bereits angegeben (sind die blauen Zahlen im Bild).

Wir teilen die absolute Häufigkeit durch die Anzahl - hier 30 - und erhalten die relative Häufigkeit.

Relative Häufigkeiten Würfelversuch:

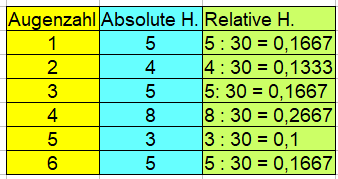
Eine kleine Kontrolle gibt es auch noch. Zählt man die relativen Häufigkeiten zusammen, kommt man in der Summe auf 1. Alternativ kann man die relativen Häufigkeiten auch in Prozent angeben. Dazu einfach die Werte mit 100 multiplizieren. Aus zum Beispiel 0,1667 würde 16,67 %.

Aufgaben / Übungen Häufigkeit

Aufgabe 1: Wie berechnet man die relative Häufigkeit? Man nimmt die absolute Häufigkeit und teilt durch ______ ?

• 1
• Gesamtzahl
• die Hälfte der Gesamtzahl
• 1 Prozent

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Häufigkeit

Fragen mit Antworten Häufigkeit